очень надо!!!!!
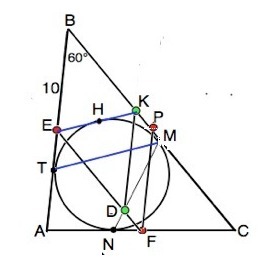
Окружность, вписанная в треугольник ABC , касается сторон BC и AC в точках M и N соответственно, E и F — середины сторон AB и AC соответственно. Прямые MN и EF пересекаются в точке D . а) Докажите, что треугольник DFN равнобедренный. б) Найдите площадь треугольника BED , если AB = 20 и ∠ABC=60°
Ответы
а) В ∆ АВС отрезок EF соединяет середины сторон АВ и АС⇒
EF– средняя линия.⇒
ЕF и ВС параллельны. Отрезок MN - секущая при них.
Соответственные углы при пересечении параллельных прямых секущей равны. ∠NDF=∠NMC
По свойству касательных из одной точки СМ=CN и ∆ МСN- равнобедренный. ⇒ углы при его основании MN равны ( свойство).
∠NDF=∠NMC; ∠NMC=∠MNC ⇒
∠NDF=∠MNC. По признаку равнобедренного треугольника МF=DF.
∆ MDF- равнобедренный.
б)На ВС отметим середину Р и проведем РF.
PF соединяет середины сторон треугольника, ⇒ PF параллельна АВ и равна АВ:2
PF=ВЕ=10
В четырёхугольнике ВЕFP противоположные стороны взаимно параллельны. ⇒
ВЕFP – параллелограмм
Из т.D проведем DK║PF и получим параллелограмм DKPF., DK=PF=BE
Отметим на АВ точку касания с окружностью буквой Т
Проведем ЕК. Для ∆ ВЕК окружность - вневписанная.
Отметим на ЕК точку Н - точку касания с окружностью.
ЕТ=ЕН, HК=KN, а так как ВТ=ВN, то ЕТ=КN ( расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением его боковой стороны равно полупериметру )=>
ВК=ВЕ=10 (из равных отрезков ВТ и ВN- вычли равные ЕТ и КN)
Но ВК=ЕD. Параллелограмм ВЕDК - ромб.
S (BEDK)=BE²•sin∠EBK=100•√3/2=50√3
S(BED)=S(BEDK):2=25√3 (ед. площади)