В трапеции ABCD основания AD и ВС относятся как 5 : 3 , а сумма углов при основании равна 90". Найдите радиус окружности, проходящей через точки А и B и касающейся прямой CD, если ab =18

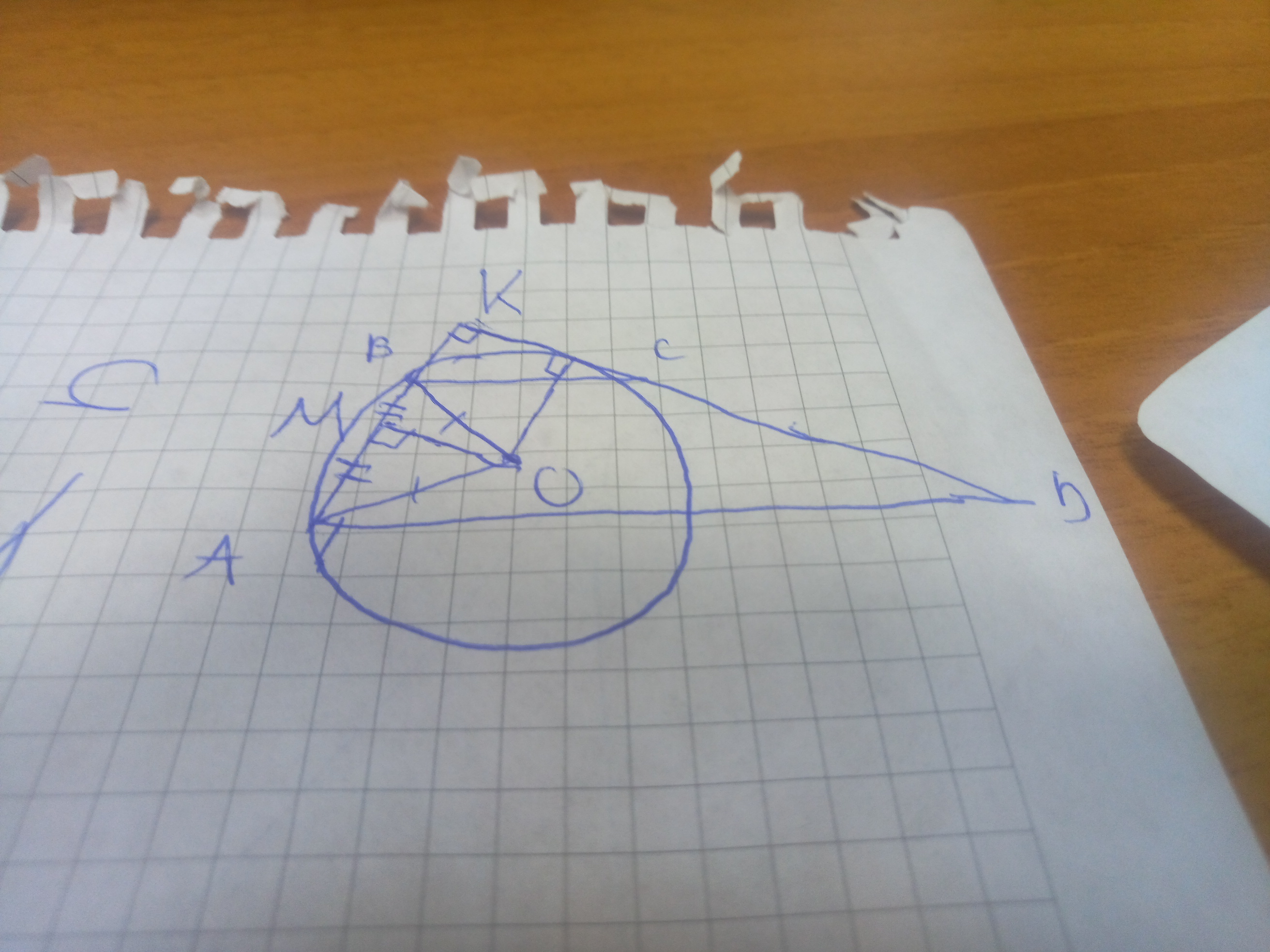
Достроим AB и DC до их пересечения в точке К. По сумме углов треугольника угол К = 180-90=90°
Проведем радиус к точке касания. Угол между ними равен 90°
Проведем радиус в точки A и В, треугольник АВО равнобедренный, его высота ОМ к основанию будет и медианой. АМ=МВ=АВ/2=9
треугольник ВКС подобен треугольнику АКО (ВС||АD, следовательно КВС = КАД как соответственные углы, угол К общий)
Пропорции сторон: ВК/АК=ВС/АD
ВК/(АВ+ВК)=ВС/АD
ВК/18+ВК=3/5
BK=27
BOCK прямоугольник тк все его углы 90°,
MK=OC=27+9=36