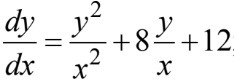Предмет: Алгебра
Автор: ActiveSync
Вопрос задан 8 лет назад

Определить тип дифференциальных уравнения и найти его решения.

Приложения:

Ответы

Ответ дал: Аноним

Тип: дифференциальное уравнение первого порядка разрешенной относительно производной, однородное.

Пусть $y=ux$ , тогда $y'=u'x+u$ получим

$u'x+u= dfrac{u^2x^2}{x^2}+8cdot dfrac{ux}{x} +12\ \ u'x+u=u^2+8u+12\ \ u'x=u^2+7u+12$

Получили уравнение с разделяющимися переменными, разделяя переменные имеем

$displaystyle int frac{du}{u^2+7u+12}=int frac{dx}{x} ;~~~Rightarrow~~~ intbigg( frac{1}{u+3}- frac{1}{u+4}bigg)du=int frac{dx}{x}$

$ln|u+3|-ln|u+4|=ln|x|+ln C\ \ ln bigg |dfrac{u+3}{u+4}bigg| =ln |xC|\ \ \ Cx=1-dfrac{1}{u+4}~~Rightarrow~~~ u+4= dfrac{1}{1-Cx} ~~Rightarrow~~ u= dfrac{4Cx-3}{1-Cx}$

Возвращаемся к обратной замене

$dfrac{y}{x} =dfrac{4Cx-3}{1-Cx}~~~Rightarrow~~~ boxed{dfrac{4Cx^2-3x}{1-Cx}}$ - общее решение

Ответ дал: Аноним

В течении 2-х часов не будет кнопка изменить)

Ответ дал: Аноним

у вас есть 2 часа до того как добавили ответ

Ответ дал: vladoleyp8x2va

т.е. через 2 часа не могу менять уже ? понял - спасибо

Ответ дал: Аноним

Да)

Ответ дал: vladoleyp8x2va

Если есть время посмотри вопрос https://znanija.com/task/29248368 типа моего постоянного клиента =) заранее спасибо.

Похожие вопросы

Английский язык