Определить стороны параллелограмма большая диагональ которого равна 14 дм, а меньшая делится перпендикуляром,опущенным на неё из вершины острого угла,на отрезки, равные 2 дм и 6 дм

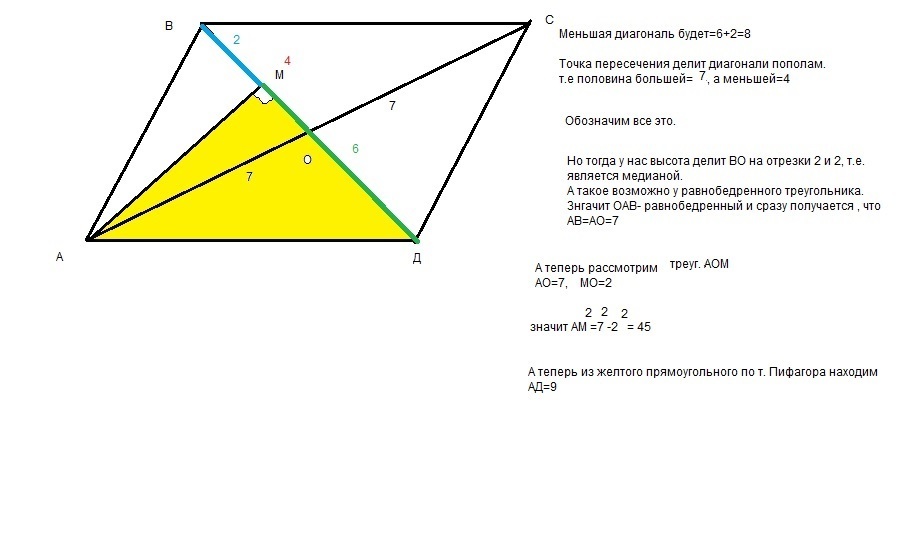
Длина короткой диагонали 2+6 = 8 дм
Диагонали точкой пересечения делятся пополам
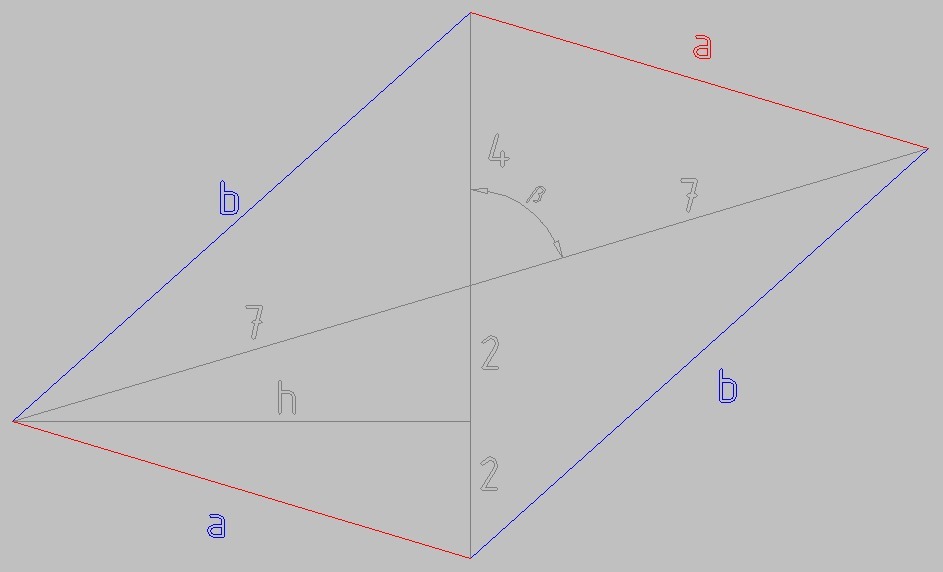
h² + 2² = a² - теорема Пифагора для 2 дм отрезка диагонали, высоты и короткой стороны
h² + 6² = b² - теорема Пифагора для 6 дм отрезка диагонали, высоты и длинной стороны
a² = 4² + 7² - 2*4*7*cos(β) - теорема косинусов для короткой стороны
b² = 4² + 7² + 2*4*7*cos(β) - теорема косинусов для длинной стороны
---
h² + 2² = a² 
h² + 6² = b² 
a² = 4² + 7² - 2*4*7*cos(β) 
b² = 4² + 7² + 2*4*7*cos(β)
---
h² + 2² = 4² + 7² - 2*4*7*cos(β) 
h² + 6² = 4² + 7² + 2*4*7*cos(β)
---
2h² + 2² + 6² = 2(4² + 7²)
2h² + 4 + 36 = 2(16 + 49)
2h² + 40 = 2*65
h² + 20 = 65
h² = 45
h = √45 = 3√5 дм
---
h² + 2² = a²
a² = 45 + 4 = 49
a = 7 дм
---
h² + 6² = b²
b² = 45 + 36 = 81
b = 9 дм

А мы, как всегда, будем идти легким путем ( ну ленивый я очень, чтобы сложно решать) :)

А мы пойдем другим путем..Решение смотри в файле...

краткость сестра таланта)) Спасибо)

нет, лень -двигатель прогресса!