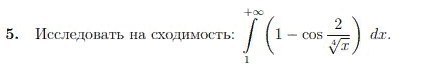Ответы
Ответ дал:
0
Здесь достаточно разложить как разность интегралов
![displaystyle intlimits^{+infty}_1 {} , dx -intlimits^{+infty}_1cos frac{2}{ sqrt[4]{x} } dx=+infty](https://tex.z-dn.net/?f=displaystyle++intlimits%5E%7B%2Binfty%7D_1+%7B%7D+%2C+dx+-intlimits%5E%7B%2Binfty%7D_1cos+frac%7B2%7D%7B+sqrt%5B4%5D%7Bx%7D+%7D+dx%3D%2Binfty "displaystyle intlimits^{+infty}_1 {} , dx -intlimits^{+infty}_1cos frac{2}{ sqrt[4]{x} } dx=+infty")
Первый интеграл будет иметь
, а значит исходный интеграл расходится (второй интеграл тоже расходится по первому признаку сравнения)
Первый интеграл будет иметь
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад