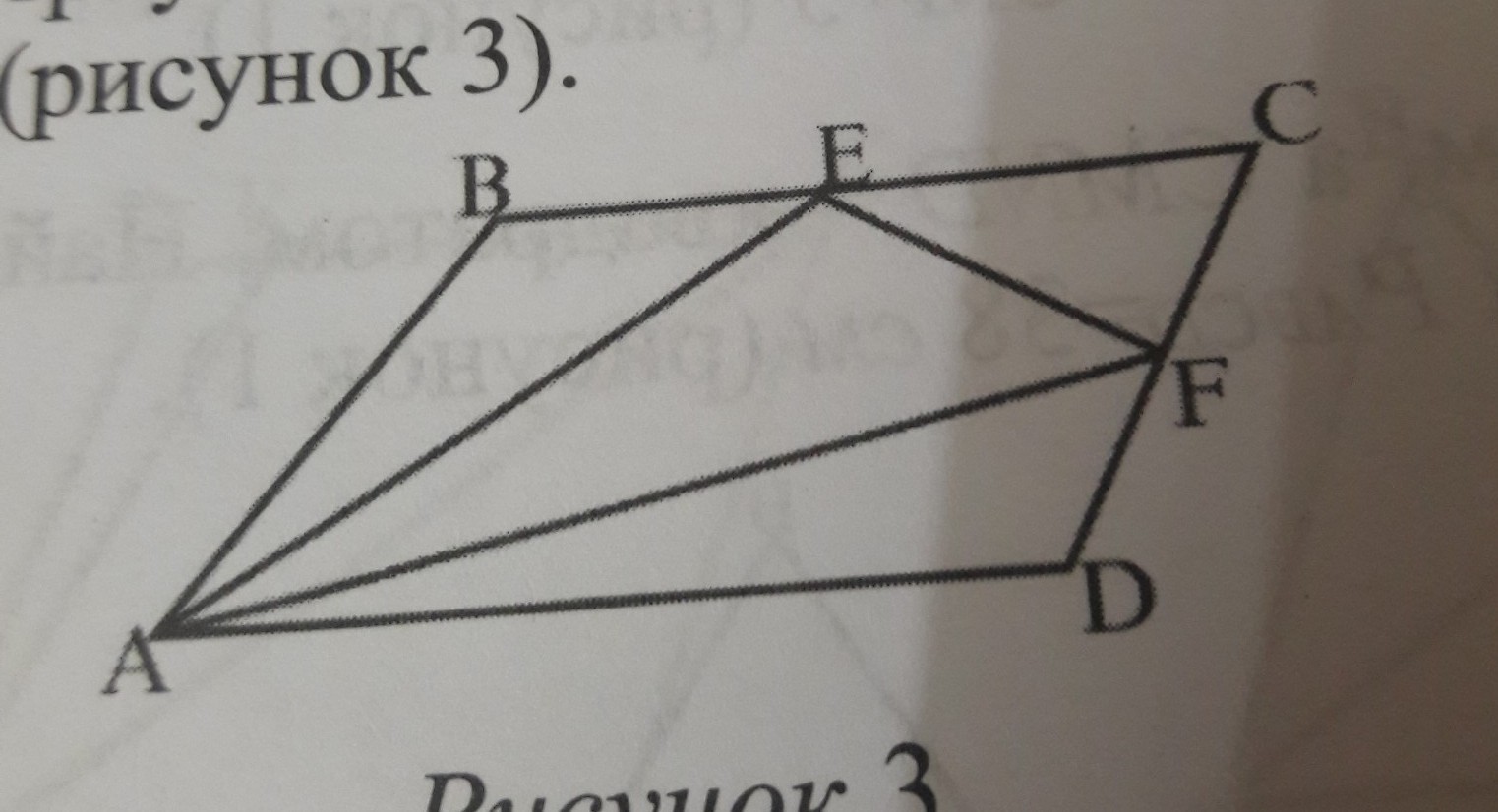
В параллелограмме ABCD, BE конгруэнто EC , CF конгруэнто FD. Найдите площадь параллелограмма , если площадь треугольника AEF равна 9 см ^2.

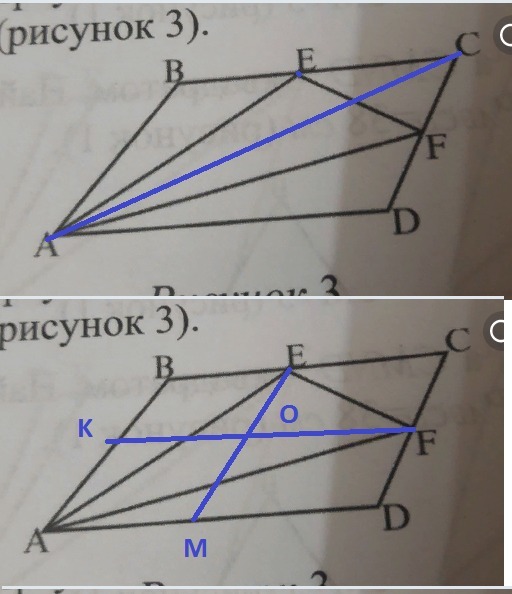
1) Проведем диагональ АС она делит паралkелограмм на 2 равных треугольника АВС и ACD ⇒SABC=SACD=(1/2)SABCD
SABE=SAEC т.к.ВЕ=ЕС и высота у них одинаковая
⇒SABE=(1/2)SABC=(1/4)SABCD
2) аналогично так как DF=FC то SAFD=(1/2)SACD=(1/4)SABCD
3) проведем средние линии ЕМ и KF они разделят ABCD на 4 равные части SOECF=(1/4)SABCD
так как EF диагональ параллелограма ECFO то
то SECF=(1/2)SOECF=(1/8)SABCD

SAEF=SABCD-SABE-SECF-SAFD=SABCD(1-1/4-1/8-1/4)=(3/8)ABCD=9
(3/8)SABCD=9
SABCD=9/(3/8)=9*(8/3)=3*8=24cм²