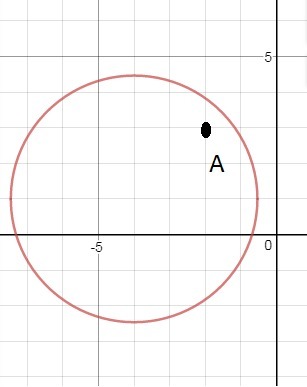
Окружность задано уравнением (x+4)²+(y-1)²=12. Как расположено точка А(-2;3) относительно этой окружности?

подставим координы точки А в уравнение
(-2+4)²+(3-1)²=2²+2²=8
так как 8<12 то точка лежит внутри окружности

СПАСИБОООО ОГРОМНОЕ

уравнение на фото

зачем 2 фото? c уравнением?

ой не туда подвесил sorry...

Найдем центр окружности:
Общее уравнение (х-х0)^2+(у-у0)^2=R^2 
O(-4,1) R=√12
Найдем расстояние от центра окружности до точки и сравним с радиусом:
OA(2,2) из конечной точки (А) вычитается начальная точка (O)
|OA|=√(x2-x1)^2+(y2-y1)^2=√2^2+2^2=√8=
√8<√12 т.е точка находиться в окружности
Обрати внимание на выделенное:
1)Если ты нашел координ. вектора то можешь сразу возвести в квадрат каждое и проссумировать под корнем
2)Если лень искать использую формулу:√(x2-x1)^2+(y2-y1)^2 
1 координаты первой точки(О) 2-координаты второй точки (А)