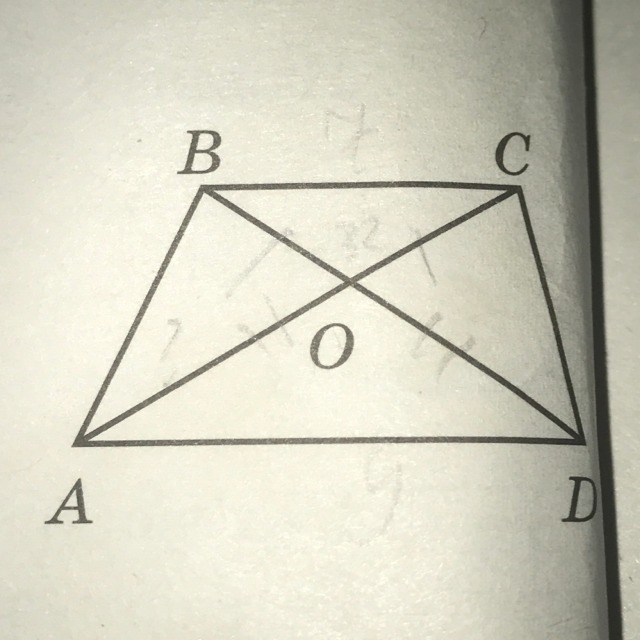
Диагонали АС и ВD в трапеции ABCD с основаниями BС и AD пересекаются в точке О.
ВС=7, АD=9, AC=32.
Найдите АО.
Приложения:
Ответы
Ответ дал:
0
ΔВОС подобен ΔАОВ по свойству диагоналей трапеции
Отсюда справедливо отношение
ВСАД=ОСАО
Пусть АО=х, тогда ОС=32-х
79 = (32-х)х
7х=288-9х
16х=288
х=18.
АО=18 ед.
Отсюда справедливо отношение
ВСАД=ОСАО
Пусть АО=х, тогда ОС=32-х
79 = (32-х)х
7х=288-9х
16х=288
х=18.
АО=18 ед.
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад