Посчитать МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ выиграша в игре

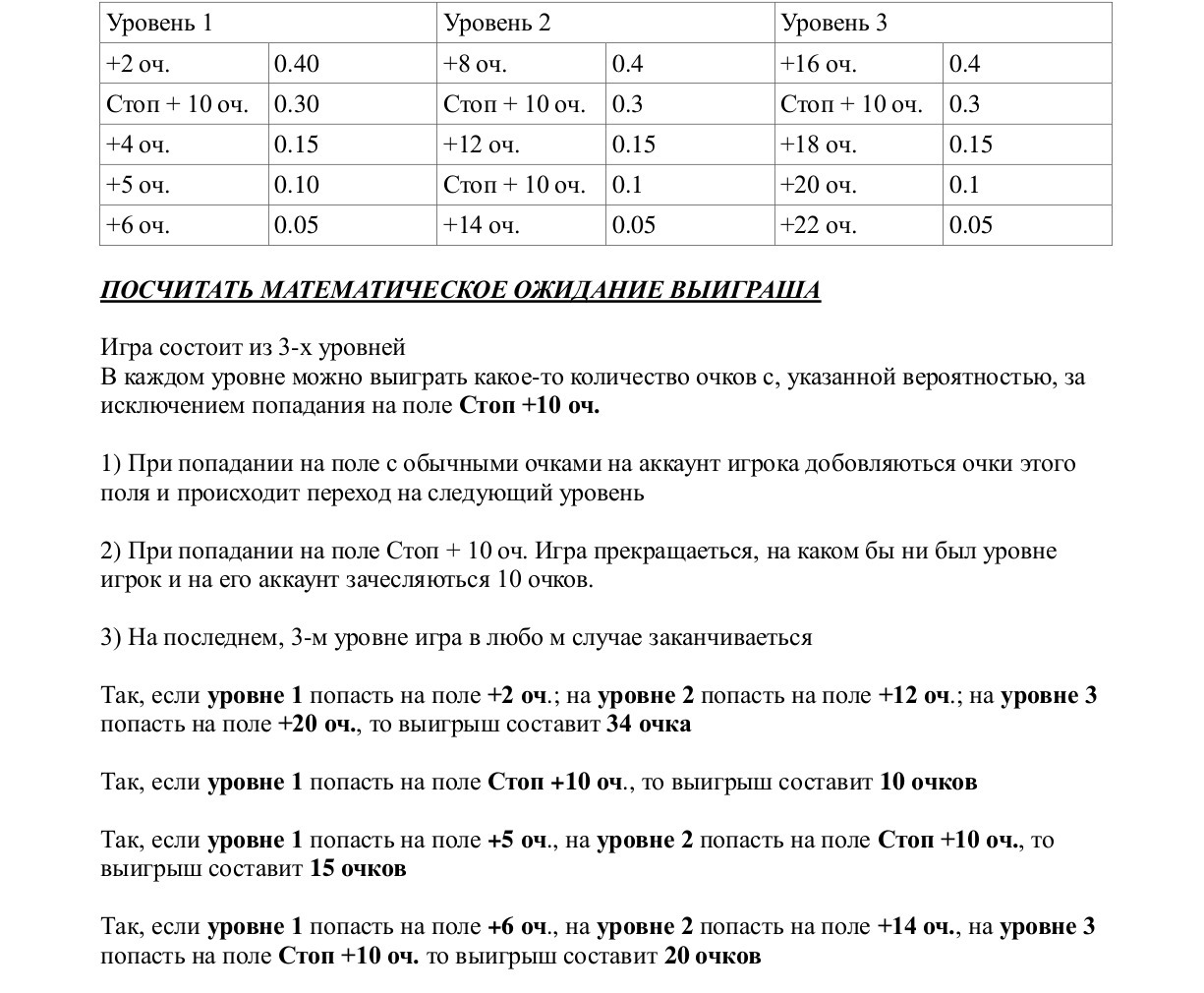
все детали игры в прикрепленной картинке
в pdf документе таже информация, что и в картинке

считать не обязательно, главное, прошу, показать как считать в таком случае, по факту у меня проблема с подсчетом мат.ожидания событий с условными вероятностями, есть идея нормировать вероятности, при переходе к следующим после первого уровням

Решим почти "в лоб":
Проще всего с третьим уровнем, на нём "стоп" ничего не меняет – игра в любом случае остановится, так что матожидание можно считать по обычной формуле . На третьем уровне матожидание прибавления числа очков игрока, дошедшего до этого уровня, будет равно


Второй уровень: с вероятностью 0.3 + 0.1 = 0.4 игрок попадёт на ячейку "стоп", получит 10 очков и закончит игру, с вероятностью 1 - 0.4 = 0.6 получит некоторое количество очков и перейдет на третий уровень, где получит в среднем 15.2 очка. Тогда матожидание изменения числа очков игрока, дошедшего до этого уровня, выражается так: 


Аналогично, для игрока, который играет на первом уровне, ожидаемое число очков равно

Огромное спасибо, я писал строчку 2*0.4+4*0.15+5*0.10+6*0.05+0.7*(и тут замирал)

можете еще с одной задачей помочь, точнее хочу свериться, возможно увидеть другое решение