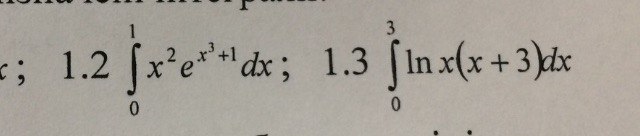Предмет: Математика
Автор: zhenya1337228
Вопрос задан 8 лет назад

1 решить методом подстановки, а 2 методом по частями

Приложения:

Ответы

Ответ дал: NNNLLL54

$1); ; int x^2cdot e^{x^3+1}, dx=[, t=x^3+1; ,; dt=3x^2, dx; ,; x^2, dx=frac{dt}{3}, ]=\\=frac{1}{3}int e^{t}, dt=frac{1}{3}, e^{t}+C=frac{1}{3}cdot e^{x^3+1}+C, ;$

$intlimits^1_0, x^2cdot e^{x^3+1}, dx=(frac{1}{3}cdot e^{x^3+1})Big |_0^1= frac{1}{3}cdot (e^2-e^1)=frac{1}{3}cdot (e^2-e); .$

$2); ; int (x+3)cdot lnx, dx=[, u=lnx; ,; du=frac{dx}{x},; v=int (x+3)dx=\\=frac{(x+3)^2}{2}, ]=frac{(x+3)^2}{2}cdot lnx-intfrac{(x+3)^2, dx}{2x}=frac{(x+3)^2}{2}cdot lnx-\\-frac{1}{2}intfrac{x^2+6x+9}{x}, dx=frac{(x+3)^2}{2}cdot lnx-frac{1}{2}int (x+6+frac{9}{x})dx=$

$=frac{(x+3)^2}{2}cdot lnx-frac{1}{2}cdot (frac{x^2}{2}+6x+ln|x|)+C, ;\\ intlimits_1^3, (x+3)cdot lnx, dx=Big (frac{(x+3)^2}{2}cdot lnx-frac{1}{2}cdot (frac{x^2}{2}+6x+ln|x|)Big )Big |_1^3=\\=18,ln3-frac{1}{2}cdot (4,5+18+ln3)-8, ln1-frac{1}{2}cdot (frac{1}{2}+6+ln1)=\\=17,5, ln3-14,5, ;$

Во 2 примере нижний предел не может быть 0, т .к. ln0 не существует (ошибка или описка в условии). Поэтому нижний предел положила
равным 1.

Похожие вопросы

Английский язык

2 года назад

Вставте глагол to be (am, is, are)

Українська мова

2 года назад

на який склад падає наголос у слові чотирнадцять

Литература

2 года назад

найти в "Муму" эпизод "Возвращение Муму"

Математика

2 года назад