четырехгранная крыша перекрывает площадь в 31 кв м. Все скаты крыши наклонены к потолку под углом 34 градуса. Найти площадь крыши

найти боковую площадь правильной пирамиды
В основании квадрат со стороной √31(иначе углы были бы разные)
Боковая площадь состоит из 4 равнобедренных треугольника с основанием √31 и высотой h=(√31/2)/cos34
S=4(√31*√31/4)/cos34=31/cos34=31/0.83=37.35

Т.к. по условию все скаты находятся под одим углом, то многогранник, образованный скатами крыши и потолком является правильной четырехугольной призмой, основание такой призмы - квадрат, пусть длина его стороны = a.
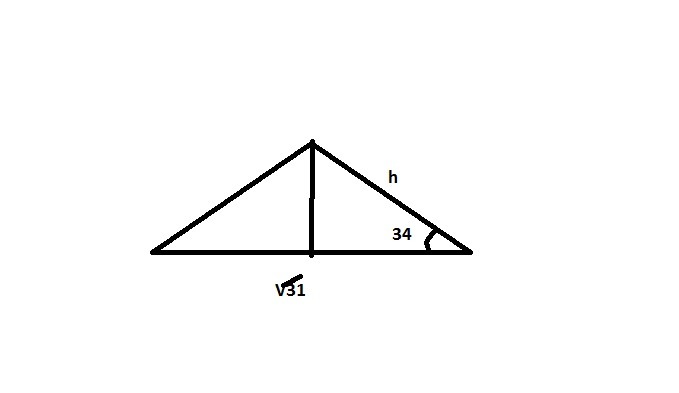
Рассмотри вертикальное сечение этой пирамиды через его вершину. Образованный треугольник - равнобедренный, имеет основание = a, пусть две другие стороны = x, тогда, опустив высоту на основание этого треугольника, найдем x = a/(2 cos 34). С другой стороны, x - высота треугольника (любого из скатов крыши), тогда площадь ската S_1 = a*x/2 = a²/(4 cos 34), а площадь всей крыши: S_4 = 4*S_1 = a²/cos 34 = S_потолка / cos 34 = 31 / 0.83 ≈ 37.3 м²