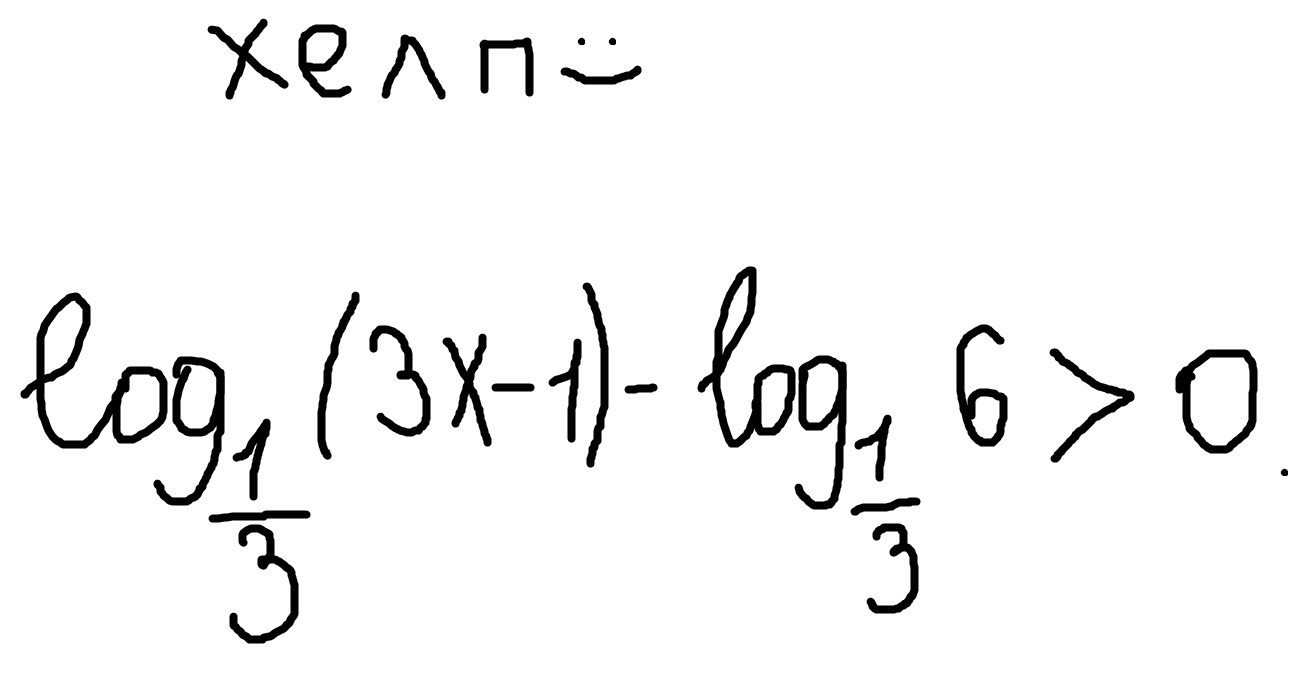Ответы
Ответ дал:
0
x€(1/3;7/3)
Ответ дал:
0
После нахождения ОДЗ, получим что x> ;
;
Перенести постоянную в правую часть и сменить её знак:
㏒ (3x-1)>㏒
(3x-1)>㏒ (6);
(6);
Для 0<a<1 выражение ㏒a (x)>㏒a (b)=x<b:
3x-1<6;
Перенести постоянную в правую часть и сменить её знак:
3x<6+1;
Сложить число после знака неравенства:
3x<7;
Разделить обе части неравенства на 3:
x< ,x>
,x> ;
;
Найти пересечение множества решений и области допустимых значений:
x∈{ ,
,  }
}
Перенести постоянную в правую часть и сменить её знак:
㏒
Для 0<a<1 выражение ㏒a (x)>㏒a (b)=x<b:
3x-1<6;
Перенести постоянную в правую часть и сменить её знак:
3x<6+1;
Сложить число после знака неравенства:
3x<7;
Разделить обе части неравенства на 3:
x<
Найти пересечение множества решений и области допустимых значений:
x∈{
Похожие вопросы
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад