Боковое ребро правильной треугольной пирамиды образует с плоскостью основания угол в 30°. Найдите тангенс угла между плоскостью боковой грани пирамиды и плоскостью ее основания.
Ответы
Ответ дал:
0
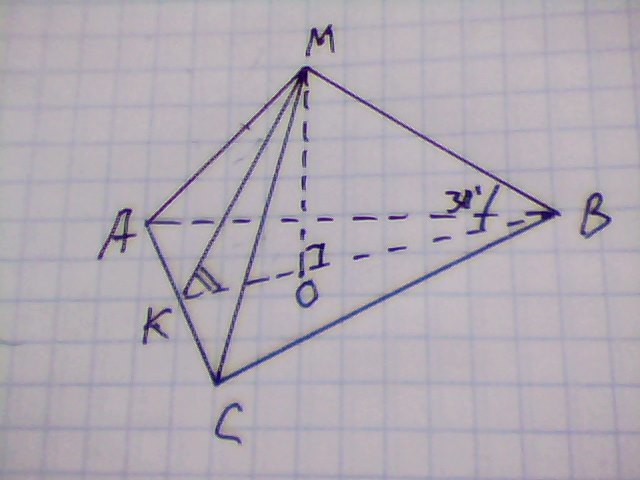
По условию АВ=ВС=АС; ∠ОКМ=30°.
ΔОМК- прямоугольный; ОМ- высота пирамиды.
Пусть ОМ=х , тогда МВ=2·ОМ=2х, ОВ²=МВ²-ОМ²=4х²-х²=3х².
ВМ=х√3. ОК=0,5ВО=х√3/2.
tg0М=ОМ/ОК=2х/х√3=2/√3.
Ответ : 2/√3.
ΔОМК- прямоугольный; ОМ- высота пирамиды.
Пусть ОМ=х , тогда МВ=2·ОМ=2х, ОВ²=МВ²-ОМ²=4х²-х²=3х².
ВМ=х√3. ОК=0,5ВО=х√3/2.
tg0М=ОМ/ОК=2х/х√3=2/√3.
Ответ : 2/√3.
Приложения:
Ответ дал:
0
в условии угол 30 градусов другой и поэтому это неверное решение
Ответ дал:
0
<МКО надо найти. Дан
Ответ дал:
0
а тогда как же правильно
Ответ дал:
0
Смотрите в ЛС.
Ответ дал:
0
tgК=2/корень из 3 Решение исправил но было поздно
Похожие вопросы
2 года назад
2 года назад
2 года назад
9 лет назад