В прямоугольном параллелепипеде АВСDА1В1С1D1 грань АВСD –квадрат со стороной 1. Боковое ребро АА1 вдвое больше ребра АВ. Через диагональ В1D и каждую точку ребра АА1 проводятся всевозможные сечения этого параллелепипеда. Определите наименьшую площадь такого сечения.
Ответы
Ответ дал:
0
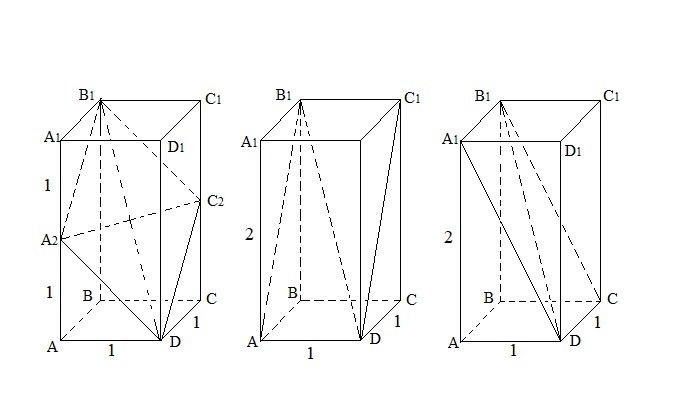
Сечениями параллелепипеда ABCDA1B1C1D1, проходящими чечез диагональ B1D и точку на диагонали AA1, будут параллелограммы с различным соотношением сторон.
Наибольшими по площади будут два прямоугольника AB1C1D и A1B1CD, а наименьшим будет ромб A2B1C2D со стороной равной меньшей диагонали (точки A2 и C2 расположены на рёбрах AA1 и CC1 соответственно).
A2C2 = A2D = √(1² + 1²) =√2;
B1D = √(1² + 1² + 2²) = √6;
S = 1/2D*d;
S A2B1C2D = 1/2√6 * √2 = √12/2 = √3.
Проверим, действительно ли площадь ромба A2B1C2D меньше площади прямоугольника AB1C1D.
AD = 1;
AB1 = √(1² + 2²) = √5;
S AB1C1D = 1 * √5 = √5.
Ответ: √3.
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад