1)f(x)=14x^6-4x^3+9x^2-x+4.
3)найдите первообраз. ф. f(x)=12x^2+4 значение которой при х=1 положительное.
4)найдите площадь криволинейной трапеции ограниченной прямыми х-3,х=2, график функции у=х^2 и осью Ох
Помогите решить домашку!!!!
Ответы
Ответ дал:
0
1.
2.
F(1) >0
4+4+C > 0 ⇒ C > - 8
О т в е т. F(x)=4x^3+4x-6 например
3.
Задание написано некорректно.
х-3 - что это?
Прямая у=х-3
Не получается фигуры, ограниченной указанными линиями. См. рис.
Приложения:
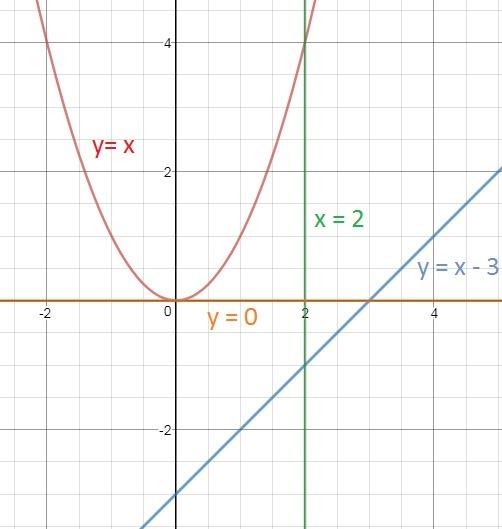
Похожие вопросы
2 года назад
2 года назад
8 лет назад