площадь треугольника образованного осями координат и прямой √2x-√6y+2√3=0 равна... 1)2√3; 2)√6 3)√3 4)√3/2 5)√6/2
Ответы
Ответ дал:
0
Для начала найдем точки пересечения прямой с осями координат:
√2x-√6y+2√3=0
при x=0 ⇒ √2*0-√6*y+2√3=0, получается y=√2
при y=0 ⇒ √2*x-√6*0+2√3=0, получается x=-√6
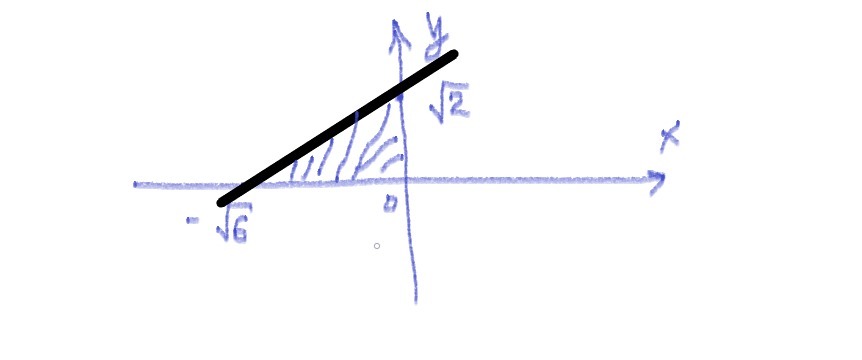
Тогда выходит треугольник (смотреть фото), катеты которого равны √2 и √6
А площадь этого треугольника мы найдем по формуле:
SΔ=1/2(a×b)=1/2(√2*√6)=√3
Ответ: √3
Приложения:
Ответ дал:
0
привет, спасибо за решение. только там (2х) все выражение под корнем и (6у) тоже все выражение под корнем.
Ответ дал:
0
Тогда x=-6, a y=2 и S=6
Ответ дал:
0
еще раз спасибо. я затупила, ты все верно написал)))
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад