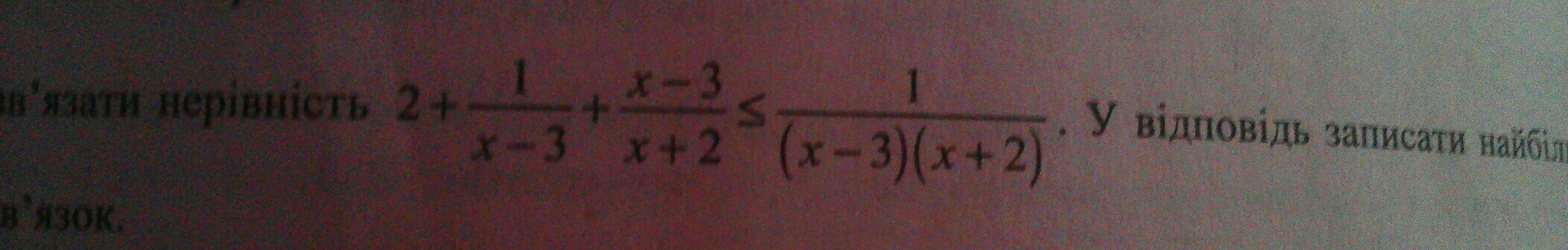Ответы
Ответ дал:
0
Х не равен 3 и -2
Методом интервалов находим промежуток и накладывая то ,чему не равен х :
Ответ дал:
0
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

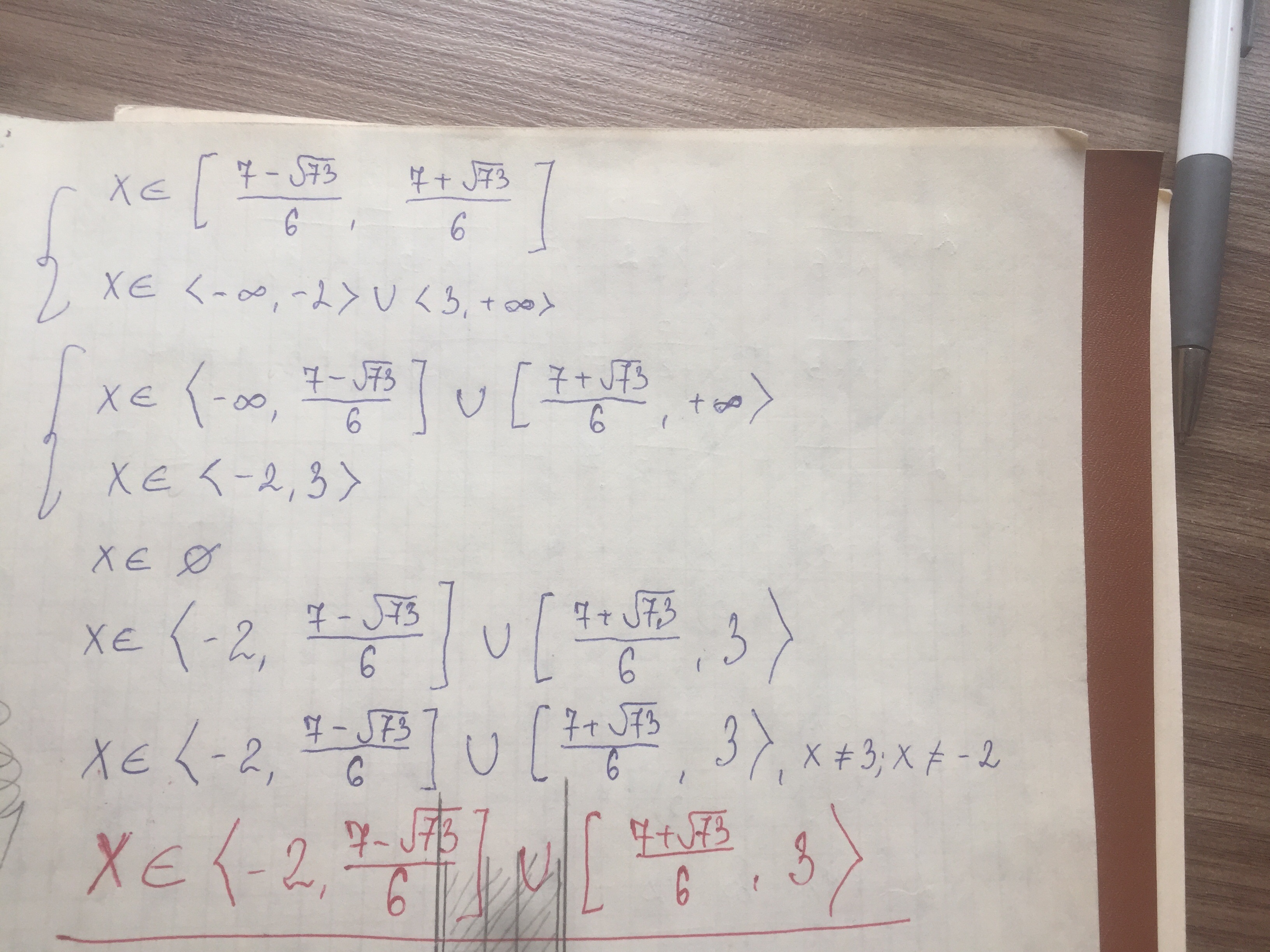
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад