Почему исчезает корень при решении уравнении  следующим образом: умножаем обе части на x+3, в итоге получаем уравнение
следующим образом: умножаем обе части на x+3, в итоге получаем уравнение  , далее заменяем
, далее заменяем  и получаем обычный квадратный трёхчлен вида
и получаем обычный квадратный трёхчлен вида  решив который получаем корни 3 и -4, но -4 не подходит, т.к. результатом арифметического квадратного корня не может быть отрицательное число, остаётся только 3 и уравнение
решив который получаем корни 3 и -4, но -4 не подходит, т.к. результатом арифметического квадратного корня не может быть отрицательное число, остаётся только 3 и уравнение  , корнями которого будут
, корнями которого будут  и
и  , но
, но  не входит в область определения, остаётся только
не входит в область определения, остаётся только  . Но вот должен быть ещё один корень: -5. Куда он делся? Я вообще всегда думал, что при умножении обеих частей на переменную количество корней может только увеличиваться, т.е. появляются побочные, но исчезать, это что-то новенькое, кто-нибудь надеюсь объяснит.
. Но вот должен быть ещё один корень: -5. Куда он делся? Я вообще всегда думал, что при умножении обеих частей на переменную количество корней может только увеличиваться, т.е. появляются побочные, но исчезать, это что-то новенькое, кто-нибудь надеюсь объяснит.
Ответы
Ответ дал:
0
могу предложить такое рассуждение:
(сейчас еще подумаю, где теряется в вашем решении...)
Приложения:
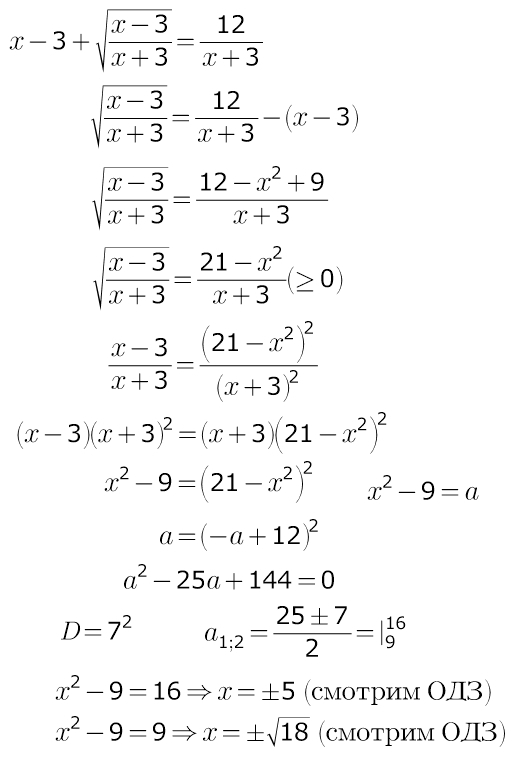
Ответ дал:
0
Интересно то, что если взять ваше 2-е действие и там домножить обе части на x+3, а затем возвести их в квадрат, то ответ получится точно таким же
Ответ дал:
0
еще интересно: мною предложенная замена и ваша очень рядом...
Ответ дал:
0
и еще можно сразу ввести замену: весь корень из дроби заменить на (а) и найти зависимость (выразить) оставшийся икс через (а)... получится то же самое и корень не потеряется...
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад