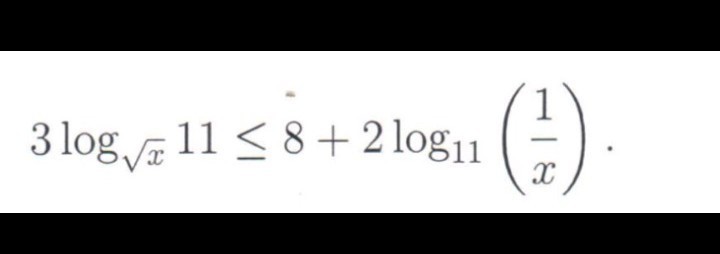Ответы
Ответ дал:
0
Найдём ограничения: х > 0 ; х ≠ 1
Пусть log₁₁(x) = a, тогда
2a + (6/a) - 8 ≤ 0
(2a² - 8a + 6)/a ≤ 0
(a² - 4a + 3)/a ≤ 0
(a - 1)(a - 3)/a ≤ 0
-------•[0]++++++•[1]-------•[3]++++++> a
[ a ≤ 0 ⇔ log₁₁x ≤ log₁₁1 ⇔ x ≤ 1
[ 1 ≤ a ≤ 3 ⇔ log₁₁11 ≤ log₁₁x ≤ log₁₁1331 ⇔ 11 ≤ x ≤ 1331
С учётом ограничений: х ∈ ( 0 ; 1 ) U [ 11 ; 1331 ]
ОТВЕТ: ( 0 ; 1 ) U [ 11 ; 1331 ]
Ответ дал:
0
нет
Ответ дал:
0
тогда где в знаменатели t?
Ответ дал:
0
Вначале учел, что х ≠ 1. log(11)x ≠ 0 ; log(11) x ≠ log(11)1 . Опускаем логарифмы, получается х≠ 1.
Ответ дал:
0
спасибо )))
Ответ дал:
0
большое )
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад