Боковое ребро правильной четырёхугольной пирамиды равно 6см и наклонено к плоскости основания под углом, равным 30° . Найдите объём пирамиды.

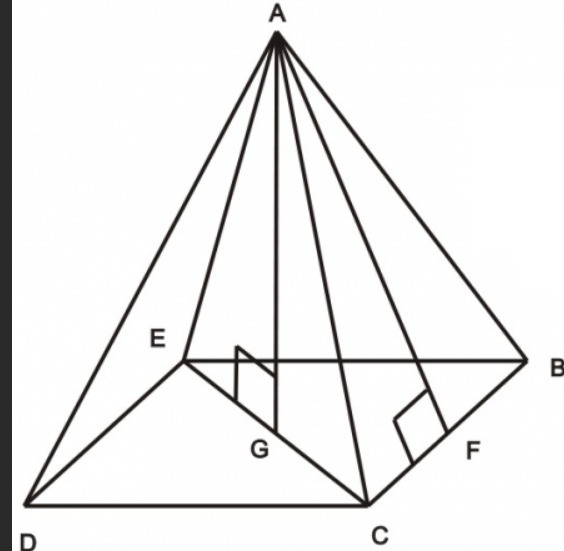
Боковое ребро, высота и половина диагонали основания образуют прямоугольный треугольник GСА,, угол GСА в нем 30*, а напротив угла в 30* находится катет равный половине гипотенузы.

АG=AC/2

AG=6/2

AG=3

Для нахождения объёма нужно знать не только высоту, но и площадь основания, по теореме Пифагора найдём её, так как второй катет равен ее половине, умножим результат на 2.

Основание правильной четырёхугольной пирамиды — квадрат, найдём его площадь через диагонали,которые между собой равны.

Теперь можем найти объём: