Через вершины А и В треугольника АВС проходит окружность радиуса 5, пересекающая сторону ВС в точке М. Найдите радиус окружности, проходящей через точки А, М и С, если АВ=6, АС=8.
Если можно с рисунком.
Ответы
Ответ дал:
0
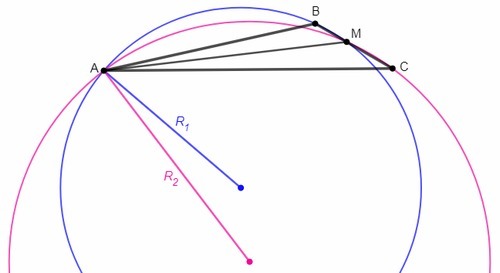
R₁ - радиус описанной окружности △AMB
R₂ - радиус описанной окружности △AMC
По теореме синусов
AB/sin(AMB) =2R₁ <=> sin(AMB)= AB/2R₁ =6/2*5 =3/5
∠AMC=180°-∠AMB
sin(AMC)= sin(180°-AMB) =sin(AMB) =3/5
AC/sin(AMC) =2R₂ <=> R₂= AC/2sin(AMC) =4*5/3 =20/3 ~6,67
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад