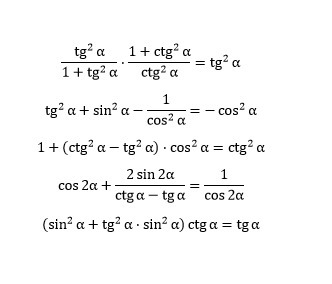Ответы
Ответ дал:
0
1.
=
=
=
=
=tg(a)²×1=tg(a)²;
2.
=
=
=
=
=
=
=
=
=-cos(a)²;
3.
1+ =
=
=
=
=
=
=
=
=
=
=
=ctg(a)²;
4.
cos(2a)+=
=
=
=
=cos(2a)+sin(2a)*tg(2a)=
=cos(2a)+
=
=
;
5.
(sin(a)²+(tg(a)·sin(a))²)·=
=(sin(a)^{2}+
=
=
=
=
=
=tg(a)
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад