< >

Найдите корни уравнения, принадлежащие отрезку [π; 2π].

cos^2x=sqrt{2} sin(2x)-sin^2x

Ответы

Ответ дал: mefody66
0

√2*sin(2x) = cos^2 x + sin^2 x = 1

sin(2x) = 1/√2

2x = (-1^n)*pi/4 + pi*n

x = (-1)^n*pi/8 + pi/2*n

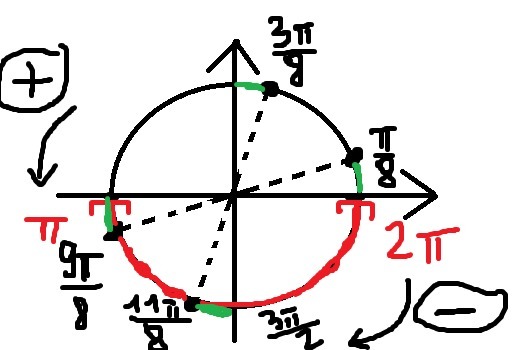
Отрезку [pi; 2pi] принадлежат корни:

x1(n=2) = pi/8 + pi = 9pi/8; x2(n=3) = -pi/8 + 3pi/2 = 11pi/8

Ответ дал: InvisorTech
0
"Найдите КОРНИ уравнения, принадлежащие ОТРЕЗКУ [π; 2π]".
Ответ дал: mefody66
0
Извиняюсь, не заметил этого условия. Это корни x1=pi+pi/8=9pi/8, x2=3pi/2-pi/8=11pi/8
Ответ дал: InvisorTech
0

cos^{2}x = sqrt{2}sin 2x - sin^{2}x \ \ 1 = sqrt{2} sin 2x \ \ sin 2x = dfrac{sqrt{2}}{2} \ \ $left[ &lt;br /&gt; begin{gathered} &lt;br /&gt; 2x = dfrac{pi}{4}+ 2pi n, n in Z \ &lt;br /&gt; 2x = dfrac{3pi}{4} + 2pi k, k in Z \ &lt;br /&gt; end{gathered} &lt;br /&gt;right.$


$left[ &lt;br /&gt; begin{gathered} &lt;br /&gt; x = dfrac{pi}{8}+ pi n, n in Z \ &lt;br /&gt; x = dfrac{3pi}{8} + pi k, k in Z \ &lt;br /&gt; end{gathered} &lt;br /&gt;right.$


Корни уравнения (1):

pi + dfrac{pi}{8} = dfrac{9pi}{8} \ \ dfrac{3pi}{2} - dfrac{pi}{8} = dfrac{11pi}{8}


Ответ: 9π/8, 11π/8

Приложения:
Похожие вопросы
Русский язык
2 года назад
ДАЮ 20 БАЛЛОВ ЗА ЗАДАНИЕ Группа ученых из США создала аппарат, способный редактировать ДНК. Работа этого аппарата напоминает редактирование текста на компьютере, когда нужно вырезать и вставить
Русский язык
2 года назад
Выберите правильную транскрипцию слова ряды. 1.[р’иды́] 2.[р’ады́] 3.[риды́]
Математика
2 года назад
хелп 2 вопрооса даю 10 баллов ​
Қазақ тiлi
2 года назад
қазақ даласының батыры жоспар құру
Математика
8 лет назад
решите уравнение а) 4(1-0,5х)=-2(3+2х) б) 5(х+1.2)=12,5х
Математика
8 лет назад
помогите пожалуйста ⏰ ⏰ со сземами каждая задача.
Физика
9 лет назад
найти потенциальную энергию тела массой 5 тонн на высоте 60 см
Литература
9 лет назад
сочинение хочу стать механиком