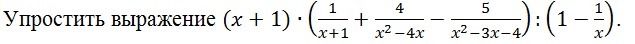Ответы
Ответ дал:
0
Ответ:..........................
Приложения:

Ответ дал:
0
Сначала упростим то,что в средних скобках

Теперь в этих же средних скобках приведем все к общему знаменателю




Теперь возьмем еще и первые скобки:

В последних скобках приведем к общему знаменателю:

И наконец:

И ОДЗ: х не равен 0, х не равен 4 и х не равен -1
Теперь в этих же средних скобках приведем все к общему знаменателю
Теперь возьмем еще и первые скобки:
В последних скобках приведем к общему знаменателю:
И наконец:
И ОДЗ: х не равен 0, х не равен 4 и х не равен -1
Приложения:

Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад