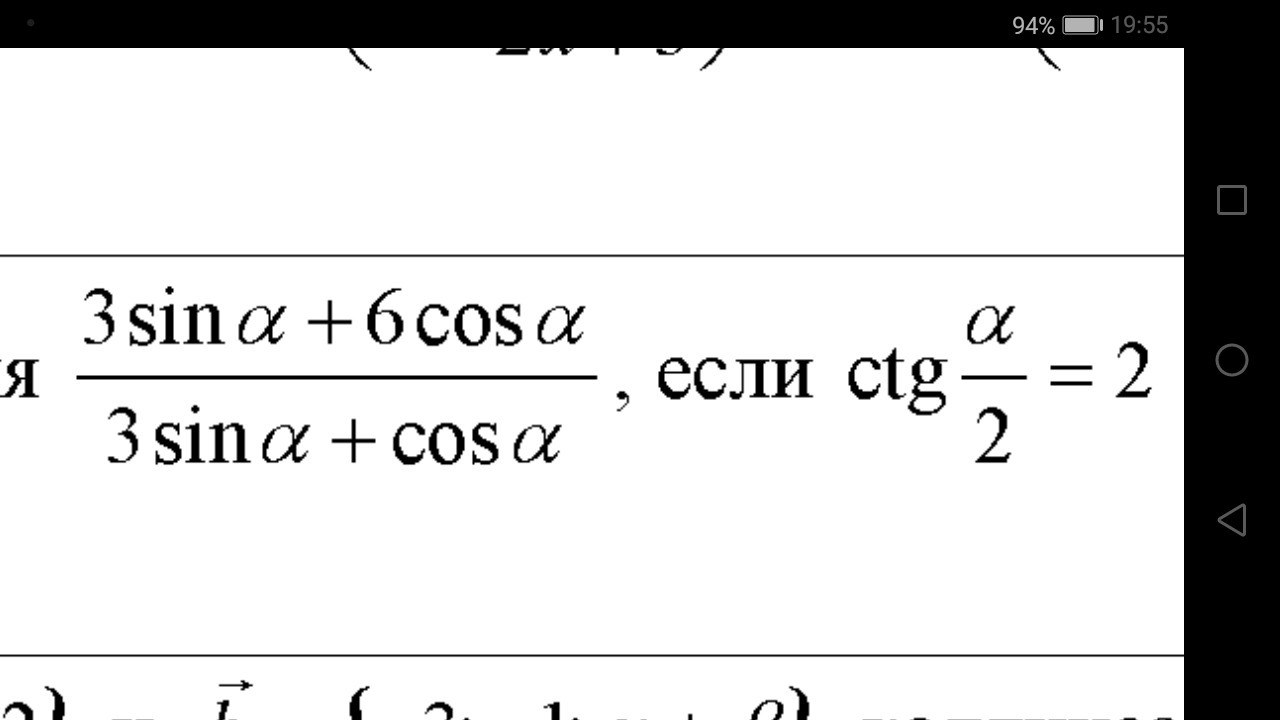Ответы
Ответ дал:
0
Используем формулу понижения степени:

Подставим теперь значения синуса и косинуса в исходное выражение:

Подставим теперь значения синуса и косинуса в исходное выражение:
Ответ дал:
0
Ответ дал:
0
Здравствуйте .Вы бы не могли бы помочь с 1 примером ?
Ответ дал:
0
Надеюсь вы вспомнили меня ))
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад