Решите тригонометрическое уравнение и найдите все корни этого уравнения принадлежащие отрезку
а)
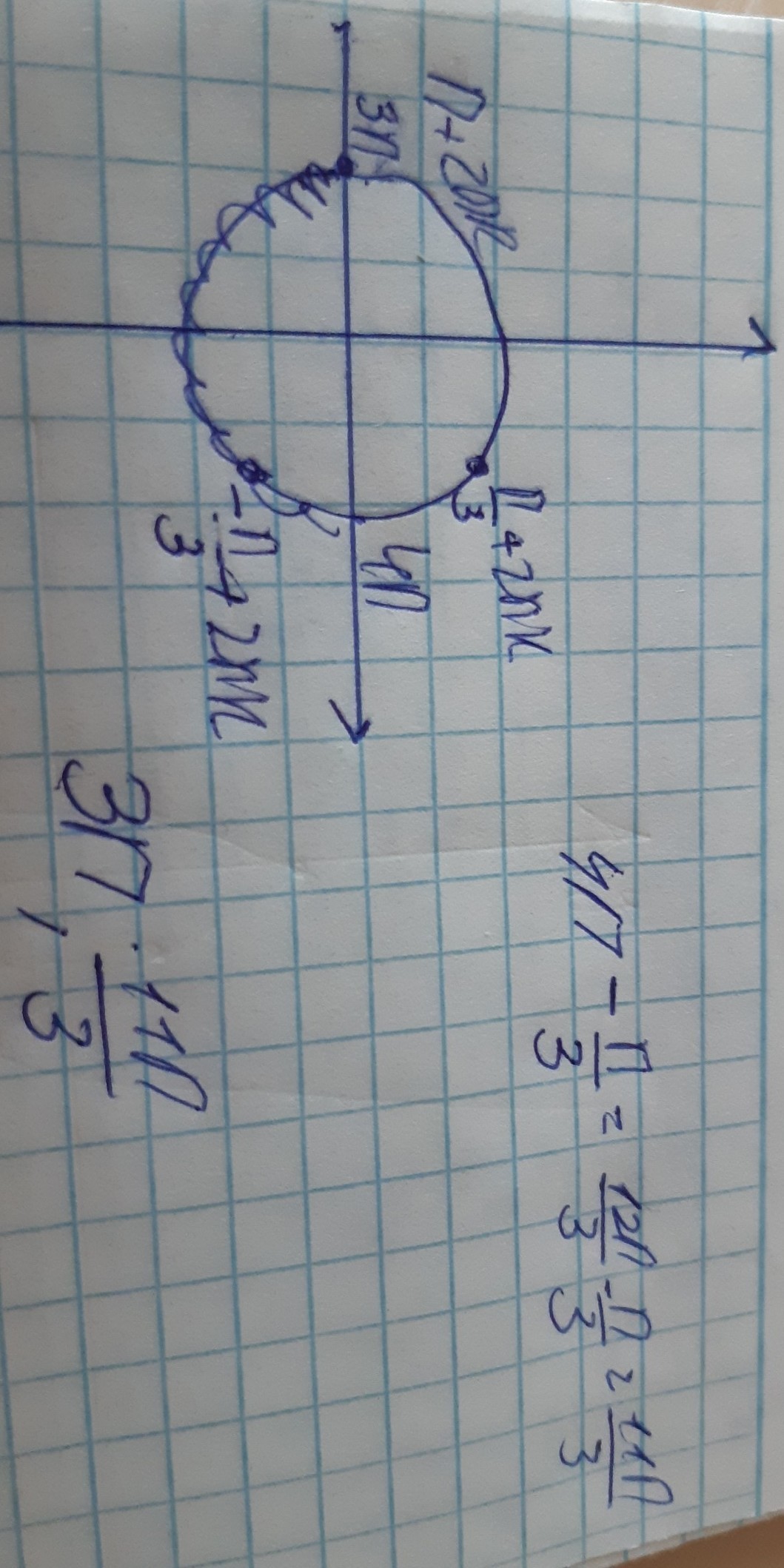
б)[3 ;4
;4 ]
]
Ответы
Ответ дал:
0
буква б во вложении
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад