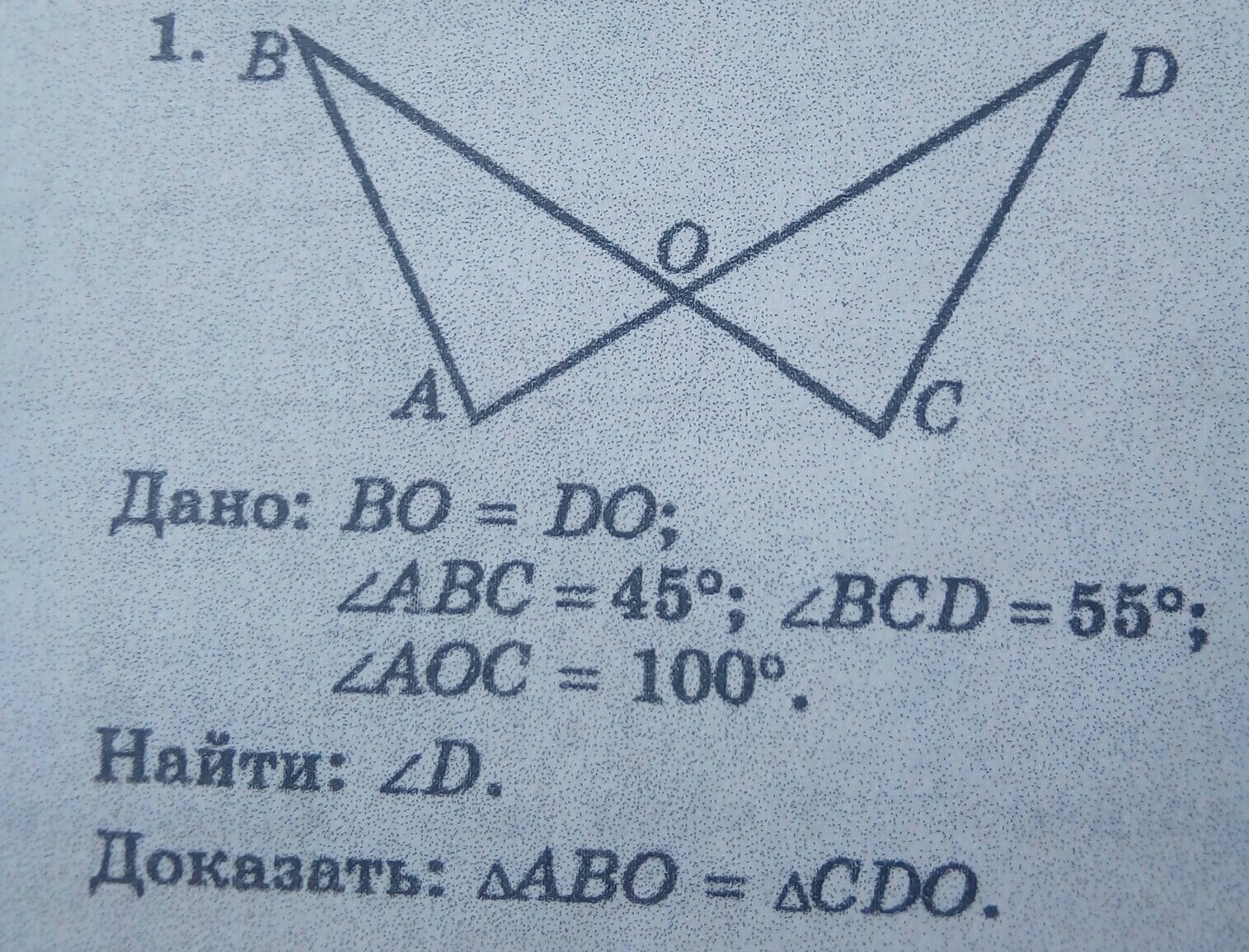помогите с геометрией

Дано: BO = DO

∠ABC = 45°

∠BCD = 55°

∠AOC = 100°

-----------------------

1) Найти ∠D

2) Доказать ΔABO = ΔCDO

1) Угол АОС - внешний угол при вершине О для треугольника ОDС. Он равен сумме двух внутренних углов BCD и D треугольника ODC, не смежных с ним:

∠АОС = ∠BСD + ∠D → ∠D = ∠AOC - ∠BCD = 100 - 55 = 45

Ответ: 45°

2) BO = DO (по условию)

∠D = ∠ABC = 45° (получено выше)

∠AOB = ∠COD (вертикальные углы)

Следовательно, ΔАВО = Δ CDO по 2-му признаку равенства треугольников, что и требовалось доказать