• Предмет: Математика
  • Автор: fotima8
  • Вопрос задан 7 лет назад
< >

сможете решить?!

intlimits^1_0 {xsqrt{1+xdx }}

Ответы

Ответ дал: Аноним
0

Это подстановка Чебышева. (Дополнительно о подстановке смотрите на фото в приложении).


Перепишем наш интеграл применив свойства степени.

displaystyleintlimits^1_0 {x(x+1)^{0.5}} , dx


Очевидно, что нам подходит 2) ведь frac{m+1}{n}=frac{1+1}{1}=2inmathbb{Z} . Значит будем использовать замену x+1=t^2 и тогда, дифференцируя: dx=2tdt , получим


displaystyle intlimits^{1}_0 xsqrt{1+x}dx=-intlimits^{sqrt{2}}_1 (1-t^2)tcdot 2tdt =intlimits^{sqrt{2}}_1(2t^4-2t^2)dt=bigg(frac{2t^5}{5}-frac{2t^3}{3}bigg)bigg|^{sqrt{2}}_1=\ \ =2t^3bigg(frac{t^2}{5}-frac{1}{3} bigg)bigg|^{sqrt{2}}_1=4sqrt{2}bigg(frac{2}{5} -frac{1}{3} bigg)-2bigg(frac{1}{5}-frac{1}{3}bigg) =frac{4(sqrt{2}+1)}{15}

Приложения:
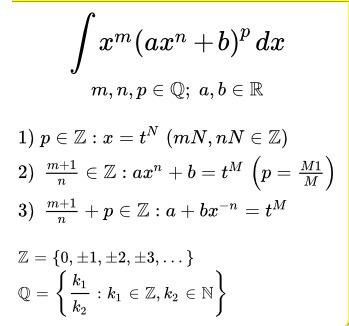
Похожие вопросы
Русский язык
2 года назад
13 слов с корнем, суффиксом и окончанием
Русский язык
2 года назад
Срочнооооооо посогите
Математика
2 года назад
4. Реши задачу. УВити в копилке лежат 2 купю- 50 руб., одна купюра 100 руб., 7 по 10 руб., 6 монет по 5 руб., 12 монет по 2 руб. и 18 монет по 1 руб. Хватит ли Вите денег на покупку Книги, если она
Информатика
2 года назад
вопрос на картинке. помогите пожалуйста (((​
Биология
8 лет назад
Организмы имеющие только доминантный или только рецессивные аллельные гены называются...
Математика
8 лет назад
построить график функции 1/2 в степени х+3
Алгебра
9 лет назад
сократите дробь х^2+10x+25/3x^2+14x-5
Математика
9 лет назад
На сколько нужно увеличить каждое число: 9,2,3,5,6,4,7 чтобы получить число 10