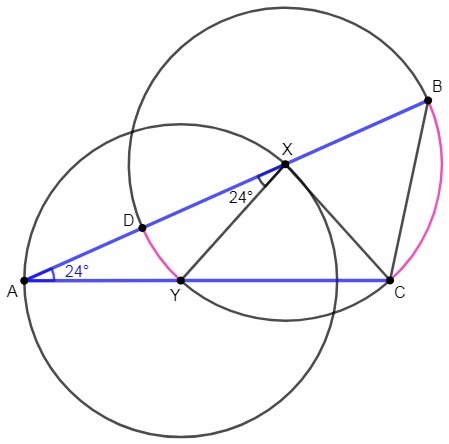
В треугольнике АБС с углом ВАС, равным 24 градусам, на сторонах АВ и АС взяты точки X и Y соответственно. При этом окружность с центром в Y, проходящая через А, проходит также через X, а окружность с центром в X, проходящая через В, проходит также через С и Y. Найдите ∠АВС.
Ответы
Ответ дал:
0
YA=YX (радиусы), △AYX - равнобедренный, ∠AXY=∠A
Центральный угол равен дуге, на которую опирается.
∪DY=∠DXY=∠A
Угол между секущими равен полуразности высекаемых дуг.
∠A= (∪BC-∪DY)/2 <=> ∪BC=2∠A+∪DY =3∠A
∠BXC=∪BC=3∠A
XB=XC (радиусы), △BXC - равнобедренный, ∠B=∠BCX
∠B=(180°-∠BXC)/2 = 90° -3/2 ∠A =54°
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад