Ответы
Ответ дал:
0
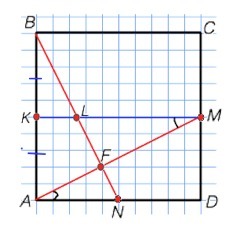
Изобразите на клетчатой бумаге квадрат ABCD со сторонами в 10 шакго сетки. Пусть М - середина CD, N– середина AD, и отрезки АМ и ВN пересекаются в точке F. Объясните, почему FM=1,5 AF.
------------------
Начертим квадрат ABCD. Отметим середину АВ точкой К и проведем КМ. Точку пересечения КМ и ВN обозначим L.
КМ проходит через середины АВ и CD, КМ║AD
В ∆ АВN KL- средняя линия и равна половине AN:2==5:2=2,5 ⇒
LM=10-2/5=7,5
КМ║AD по построению, АМ - секущая. ⇒
в ∆ LFM и ∆ AFN углы М и А равны (накрестлежащие), углы при F равны (вертикальные).=>
∆ LFM и ∆ AFN подобны по двум углам,
KM=AD=10
AN=5
Стороны подобных треугольников пропорциональны.
AF:FM=AN:LM=5:7,5⇒
AF:FM=5:7,5
5FM=7,5AF
FM=1,5AF
Приложения:
Ответ дал:
0
Треугольники BKL BAN подобны, с коэффициентом подобия 2, значит KL в 2 раза меньше AN, то есть равно 2,5
Ответ дал:
0
автор, подобие треугольников то проходили?
Ответ дал:
0
Просьба дать решение без т.Пифагора. Оно дано.
Ответ дал:
0
Да, хорошее решение, я у автора спрашиваю, поймет ли она такое, она в 6 классе, не знаю, проходили ли они подобие
Ответ дал:
0
Нет, не проходили
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад
