Предмет: Математика
Автор: tanyatreo
Вопрос задан 8 лет назад

< >

Вычислить двойной интеграл,ограниченного заданными линиями: ∫ ∫
D
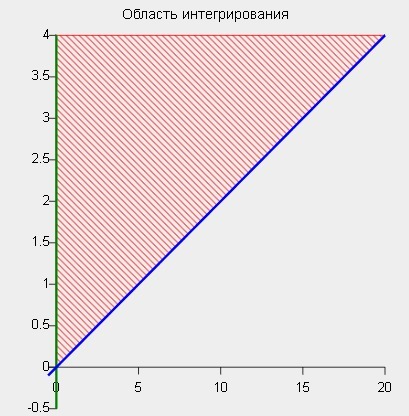
5y^2cos (xy/2)dxdy, если область D ограничена линиями D:x=0, y=4, y=x/5

Ответы

Ответ дал: Аноним

0

Интегрируем функцию $5y^2cosfrac{xy}{2}$ на множестве, заданном неравенствами $displaystyle left { {{0leq yleq 4} atop {0leq xleq 5y}} right.$

$displaystyle int int _D5y^2cosfrac{xy}{2} dxdy=intlimits^4_0 {dy} intlimits^{5y}_0 {5y^2cosfrac{xy}{2} } , dx =\ \ \ =intlimits^4_0 {bigg[10ysinfrac{xy}{2} bigg]bigg|^{5y}_0} , dy=intlimits^4_0 {10ysinfrac{5y^2}{2} } , dy=intlimits^4_0 {2sinfrac{5y^2}{2} } , dbigg(frac{5y^2}{2} bigg)=\ \ =-2cosfrac{5y^2}{2} bigg|^4_0=-(-2)-2cos 40=2-2cos40$

Приложения:

Похожие вопросы

Другие предметы

2 года назад

Почему иконы являются для христиан святыней

Английский язык

2 года назад

помоги ответить на вопрос 3и4

Математика

2 года назад

ПОМОГИТЕ ПЛИЗ.Поні, пробігаючи по колу арени цирку 6 разів, долає відстань, що приблизно дорівнює 301,44 м. Знайдіть площу арени. Всі обчислення виконуйте з точністю до сотих.

Русский язык

2 года назад

Пожалуйста Кщккщкщащрщмщсщащаащашушувввв

Математика

8 лет назад

как решать? как делать таблицу?

Литература

8 лет назад

Помогите пожалуйста

Физика

9 лет назад

из пункта а в пункт b ,расстояние между которыми 100 км навстречу друг другу выехали два автомобиля со скоростями 110 км/ч и 25 м/с.через сколько встречается автомобили??

География

9 лет назад

Что означает слово «география»? 2. Кто первым применил это слово? 3. Что изучает физическая география? 4. Каким образом человек накапливал знания о Земле? 5. Из каких источников можно получать