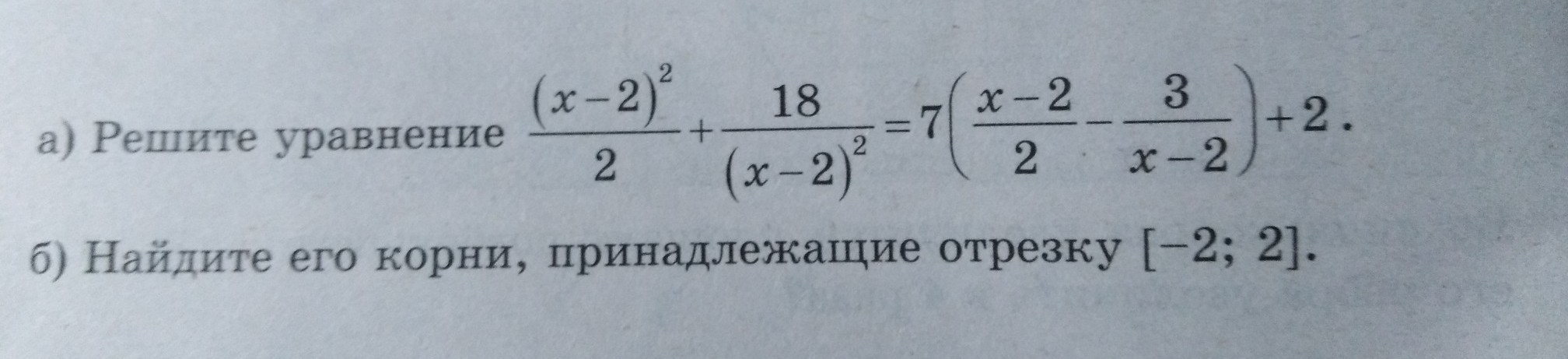Ответы
Ответ дал:
0
А)

О.Д.З. : х ≠ 2
Сделаем замену : Пусть

Возведем обе части в квадрат:

Домножим обе части уравнения на 2 :
( х - 2 )²/ 2 + 18/ ( х - 2 )² = 2( t² + 3 )
Подставляем в исходное уравнение :

Обратная замена:

Домножим на 2( х - 2) :


Домножи на 2( х - 2 ) :

Б ) [ - 2 ; 2 ]
Для начала сравним найденные корни и покажем их на числовой прямой:

____• [ -2 ]____• [ - 1 ]_____•[ 6 - √22 ]______• [ 2 ]_______• [ 4 ]_______• [ 6 + √22 ]_____ Х
Принадлежат данному промежутку только корни -1 и 6 - √22
ОТВЕТ: а) - 1 ; 4 ; 6 - √22 ; 6 + √22 ; б) - 1 ; 6 - √22
О.Д.З. : х ≠ 2
Сделаем замену : Пусть
Возведем обе части в квадрат:
Домножим обе части уравнения на 2 :
( х - 2 )²/ 2 + 18/ ( х - 2 )² = 2( t² + 3 )
Подставляем в исходное уравнение :
Обратная замена:
Домножим на 2( х - 2) :
Домножи на 2( х - 2 ) :
Б ) [ - 2 ; 2 ]
Для начала сравним найденные корни и покажем их на числовой прямой:
____• [ -2 ]____• [ - 1 ]_____•[ 6 - √22 ]______• [ 2 ]_______• [ 4 ]_______• [ 6 + √22 ]_____ Х
Принадлежат данному промежутку только корни -1 и 6 - √22
ОТВЕТ: а) - 1 ; 4 ; 6 - √22 ; 6 + √22 ; б) - 1 ; 6 - √22
Ответ дал:
0
спасибо большое
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад