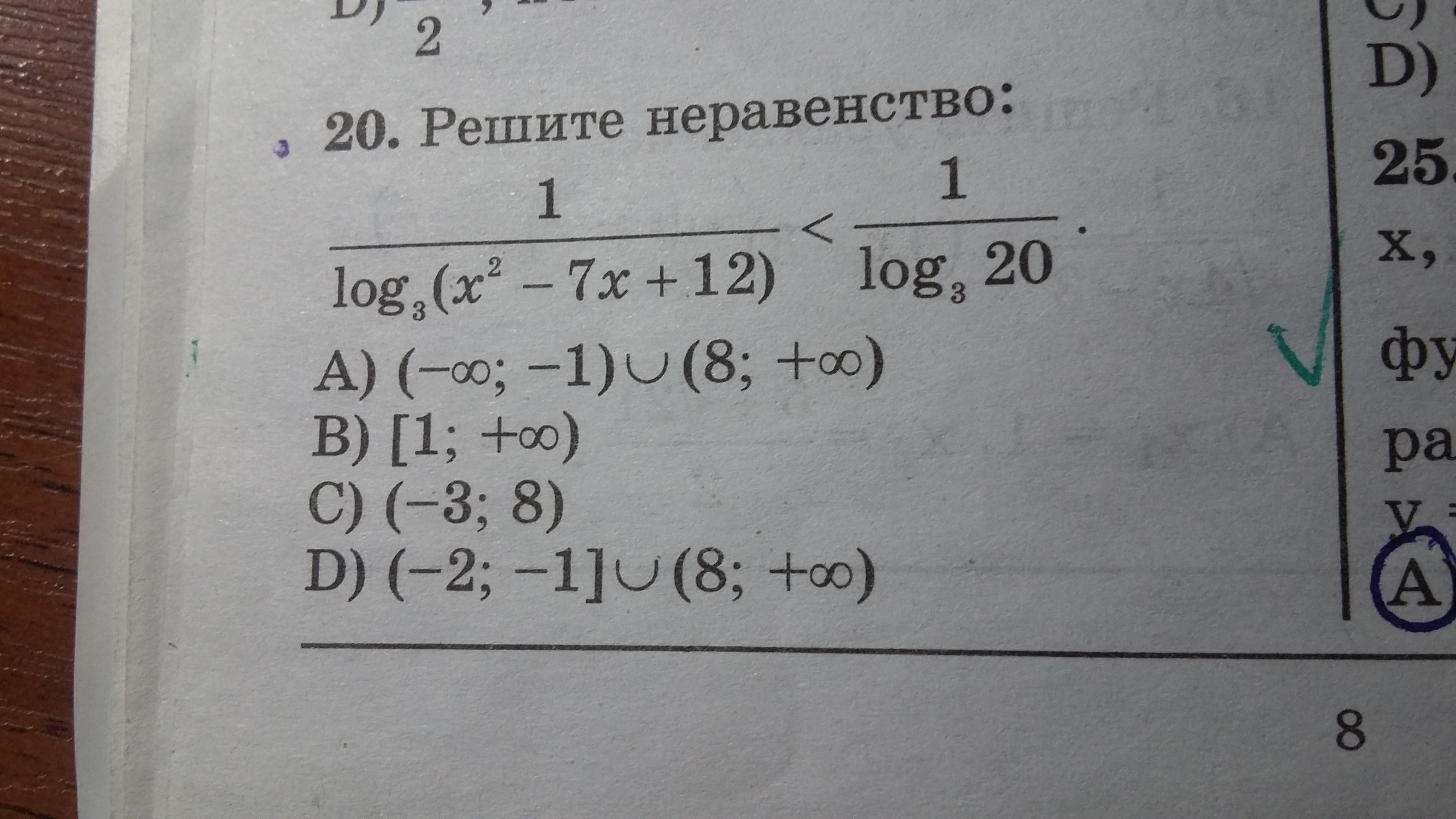ЗДРАВСТВУЙТЕ! ПОМОГИТЕ РЕШИТЬ ПРИМЕР ПОДРОБНО С РЕШЕНИЕМ. ЗАРАНЕЕ СПАСИБО.

Поскольку log3 20 > 0, возможны два случая:

log3 (x^2 - 7x + 12) < 0

log3 (x^2 - 7x + 12) > log3 20.

Первый случай:

log3 (x^2 - 7x + 12) < 0

0 < x^2 - 7x + 12 < 1

x^2 - 7x + 12 > 0

x^2 - 7x + 12 = 0

По теореме Виета:

x = 3

x = 4

x є (-оо; 3) U (4; +oo)

x^2 - 7x + 12 < 1

x^2 - 7x + 11 < 0

x^2 - 7x + 11 = 0

D = 49 - 44 = 5

x = 7-sqrt5 / 2

x = 7+sqrt5 / 2

x є (7-sqrt5 / 2; 7+sqrt5 / 2)

Решением первого случая есть пересечение (-оо; 3) U (4; +oo) и (7-sqrt5 / 2; 7+sqrt5 / 2). Поэтому x є (7-sqrt5 / 2; 3) U (4; 7+sqrt5 / 2).

Второй случай:

log3 (x^2 - 7x + 12) > log3 20

x^2 - 7x + 12 > 20

x^2 - 7x - 8 > 0

x^2 - 7x - 8 = 0

По теореме Виета:

x = -1

x = 8

x є (-оо; -1) U (8; +oo)

Общим решением неравенства есть объединение решений двух рассмотренных случаев:

x є (-оо; -1) U (7-sqrt5 / 2; 3) U (4; 7+sqrt5 / 2) U (8; +oo).