Предмет: Информатика
Автор: Dragun228
Вопрос задан 8 лет назад

< >

Задача с таблицей истинности, ответ 011, мне нужно только подробное решение!

Приложения:

Ответы

Ответ дал: krenovut

0

Берем и подставляем.

$F = 1 Rightarrow \ <br />1 = lnot x1 cap 1 cup x1 cap 0 cup x1 cap 0 cup 0 \ <br />X cap 1 = X \<br />X cap 0 = 0 Rightarrow \<br />1 = lnot x1 cup 0cup 0 cup 0 \ <br />cup = or Rightarrow \ <br />1 = lnot x1 cup 0 \ <br />x1 = 0 Rightarrow lnot x1 = 1 Rightarrow \ <br />1 = 1cup 0 Rightarrow 1 = 1 <br />$

И так далее Подставляем, сокращаем и получаем то что нужно. Знать надо обычные правила преобразования логических выражений.

Во второй строке получаем все тоже самое, но $F = 0$ . Больше там ничего не меняется, следовательно $x1 = 1$

$F = 1 Rightarrow \ <br />1 = 1 cap x2 cup 0 cap 0 cup 0 cap 0 cup 0 \ <br />X cap 1 = X \<br />X cap 0 = 0 Rightarrow \<br />1 = x2 cup 0cup 0 cup 0 \ <br />cup = or Rightarrow \ <br />1 = x2 cup 0 \ <br />x2 = 1 Rightarrow 1 = 1$

Ответ дал: DonPedro80

0

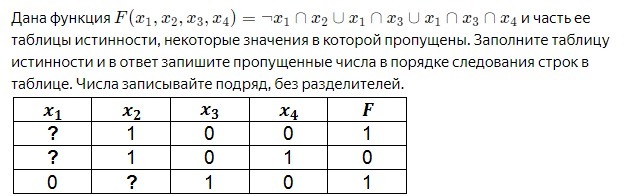
Для начала попытаемся функцию упростить.

$lnot x_1land x_2lor x_1 land x_3lor x_1land x_3land x_4=overline{x_1}x_2+x_1x_3+x_1x_3x_4=\ <br />overline{x_1}x_2+x_1x_3(1+x_4)=overline{x_1}x_2+x_1x_3$

x₄ ушло, жить стало легче.

А теперь берем каждую строку подставляем известные значения.

Для первой строки

$F=overline{x_1}x_2+x_1x_3 \ 1=overline{x_1}cdot 1+x_1cdot0\ 1=overline{x_1} to x_1=0$

Для второй строки

$F=overline{x_1}x_2+x_1x_3 \ 0=overline{x_1}cdot 1+x_1cdot0\ 0=overline{x_1} to x_1=1$

И для третьей строки

$F=overline{x_1}x_2+x_1x_3 \ 1=1cdot x_2+0cdot1 \ 1=x_2$

Ответ действительно 011.

Похожие вопросы

Қазақ тiлi

2 года назад

Мини сочинение по казахскому языку на тему: Мектеп білім ясы Прошу не использовать переводчики. За ранее спасибо

Английский язык

2 года назад

Напишите текст по вопросам на английском и переведите плииииз очень срочно вот заданиеFind some information about similar huge stones in Russia. Use the questions. 1Were can we see the stones ?

Химия

2 года назад

Визнач масову частку (%) металічного елемента у хімічній сполуці Са CO3. Пожалуста помогитееееу меня осталось 40 мин

Алгебра

2 года назад

Срочно нужно!!!!! Алгебра 7 класс

Информатика

8 лет назад

Пожалуйста, объясните как делать. :) Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6. Сколько различных вариантов шифра можно

Алгебра

8 лет назад

Помогите с заданием!!!

Математика

9 лет назад

9м=.... дм 5дм= см 35дм= ...м...дм 6дм5см=...см 80дм=...м 1м=..см 4м3дм=....дм 52см=...дм....см

Математика

9 лет назад

Решите уравнение : х+4/14=27/42