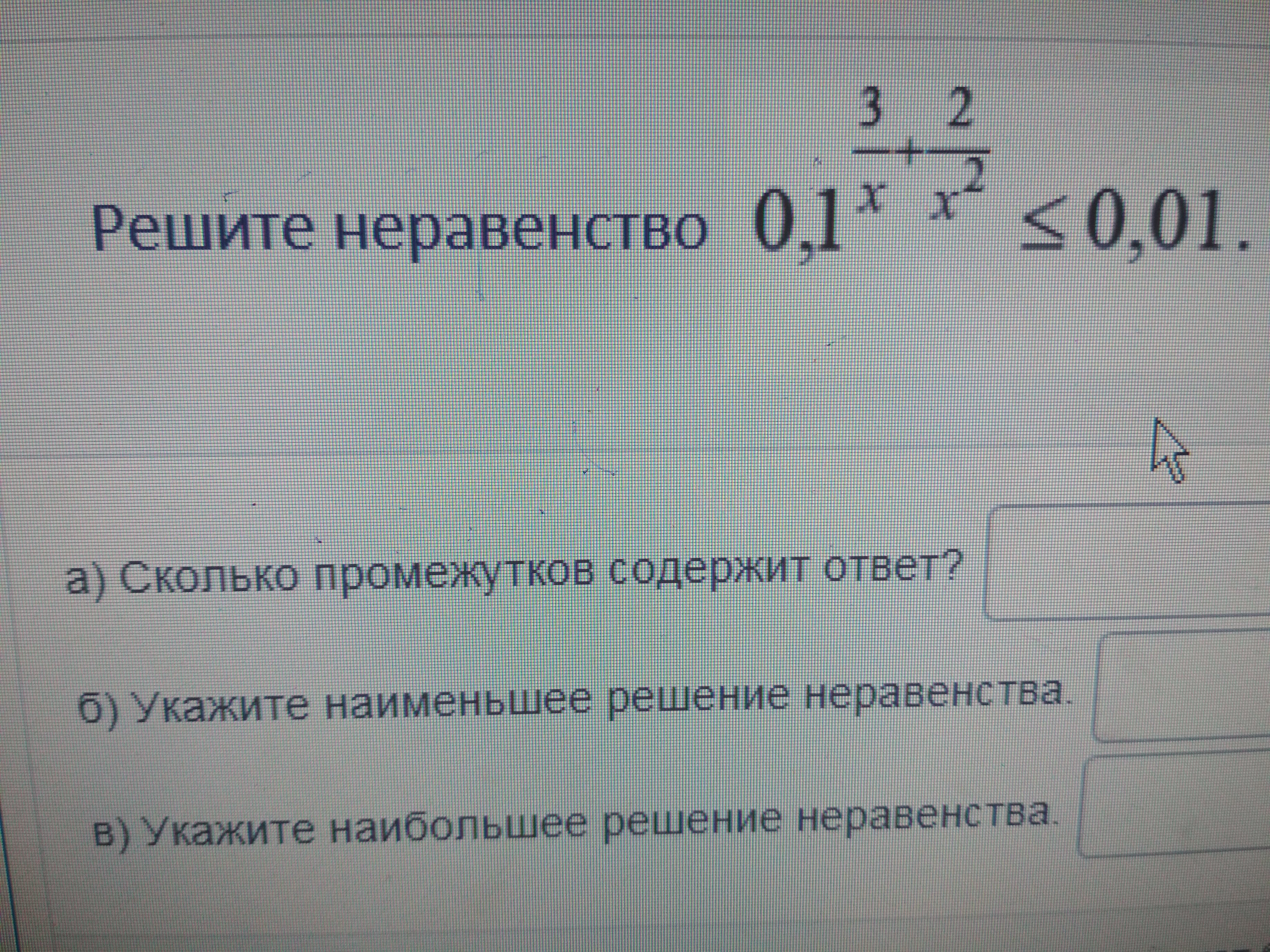
Сколько промежутков содержит ответ?
Укажите наименьшее решение неравенства
Укажите наибольшее решение неравенства

Приложения:

Ответы

Ответ дал: iosiffinikov

ОДЗ х не равен 0.

Тогда неравенство можно переписать так:

(3x+2)/x^2>=2

3x+2>=2x^2

x^2-1,5x<=1

(x-3/4)^2<=1+9/16

(x-3/4)^2<=(5/4)^2

-5/4 < = x-3/4<=5/4

-0,5<=x<=2, при этом выколота точка х=0, поэтому 2 промежутка.

Наибольшее решение неравенства х=2, наименьшее х=-0,5

Ответ дал: alkorb

$0.1 ^{ frac{3}{x} + frac{2}{ {x}^{2} }} leqslant 0.01 \ \ 0.1 ^{ frac{3}{x} + frac{2}{ {x}^{2} }} leqslant 0.1 ^{2} \ \ frac{3}{x} + frac{2}{ {x}^{2} } geqslant 2 \ \ frac{3}{x} + frac{2}{ {x}^{2} } - 2 geqslant 0 \ \ frac{3x + 2 - 2 {x}^{2} }{ {x}^{2} } geqslant 0$
Корни числителя:
-2х²+3х+2=0
D=9+4*2*2=25= 5²

$x_{1} = frac{ - 3 + 5}{ - 2 times 2} = - 0.5 \ \ x_{2} = frac{ - 3 - 5}{ - 2 times 2} = 2$

Корни знаменателя:

${x}^{2} = 0 \ x_{1} = 0 \ x_{2} = 0$
Метод интервалов:
----[-0.5]++++(0)++++[2]---->

х принадлежит [-0,5;0) U (0;2]

Ответ: а) 2; б) -0,5; в) 2

Похожие вопросы

Русский язык

2 года назад

Ночью прИшел первый замОрОзОк.Он нАдышал холОдОм на стёклА,пОсыпал зЕрнистЫм инеем на крышИ,зАхрустел под нОгами. В КАКИХ ЗНАЧИМЫХ ЧАСТЯХ СЛОВ ВЫДЕЛЕНЫ БУКВЫ?ВЫДЕЛИТЕ ЭТИ ЗНАЧИМЫЕ ЧАСТИ.ПОЧЕМУ

Русский язык

2 года назад

помогите пожалуйста! дам 20 баллов

Кыргыз тили

2 года назад

мүнөз сергек образ рахат - чыңдайт составить представление

Биология

2 года назад