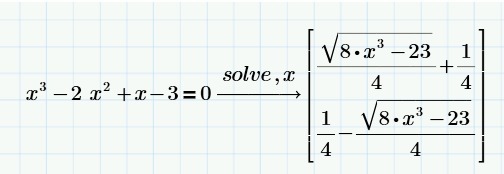Предмет: Другие предметы
Автор: Ejik17
Вопрос задан 1 год назад

Как выудить значение функции из этого решения? Символьное решение (Mathcad prime)

Приложения:

Ответы

Ответ дал: spasibo3pajbrh

Ваш Маткад как-то странно решает
Вот что получилось у меня
( с учётом иррациональных корней)
$x_{1} = - \frac{1}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}} - \frac{1}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{2}{3} + i \left(- \frac{\sqrt{3}}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}} + \frac{\sqrt{3}}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}}\right) \\ x_{2} = - \frac{1}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}} - \frac{1}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{2}{3} + i \left(- \frac{\sqrt{3}}{18 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{\sqrt{3}}{2} \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}\right) \\ x_{3} = \frac{1}{9 \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}}} + \frac{2}{3} + \sqrt[3]{\frac{\sqrt{77}}{6} + \frac{79}{54}} $

Ejik17: А у Вас решение не законченное и может быть, даже не верное

spasibo3pajbrh: Оно верное.Это метод Виетта -Кардано. а сомневаться - это вполне нормальный процесс. Если Вам интересно приблизительное значение корней , то х1,2≈ -0,00873±1,1713i x3≈2,1746

Похожие вопросы

Математика

1 год назад

Будь ласка, допоможіть

Математика

1 год назад

спростить вираз і обчислить його значення: 1)5,4а-3,9а,якщо 0,26 2)1,8m-0,5+0,7m якщо m=3,94

Математика

1 год назад

Периметр трикутника дорівнюе 46 дм.Довжина другої сторони становить 60% довжини першої, а довжина третьої сторони- 7/10 від першої.Знайди довжину другої сторони трикутника, (помогите пожалуйста)

Английский язык

1 год назад