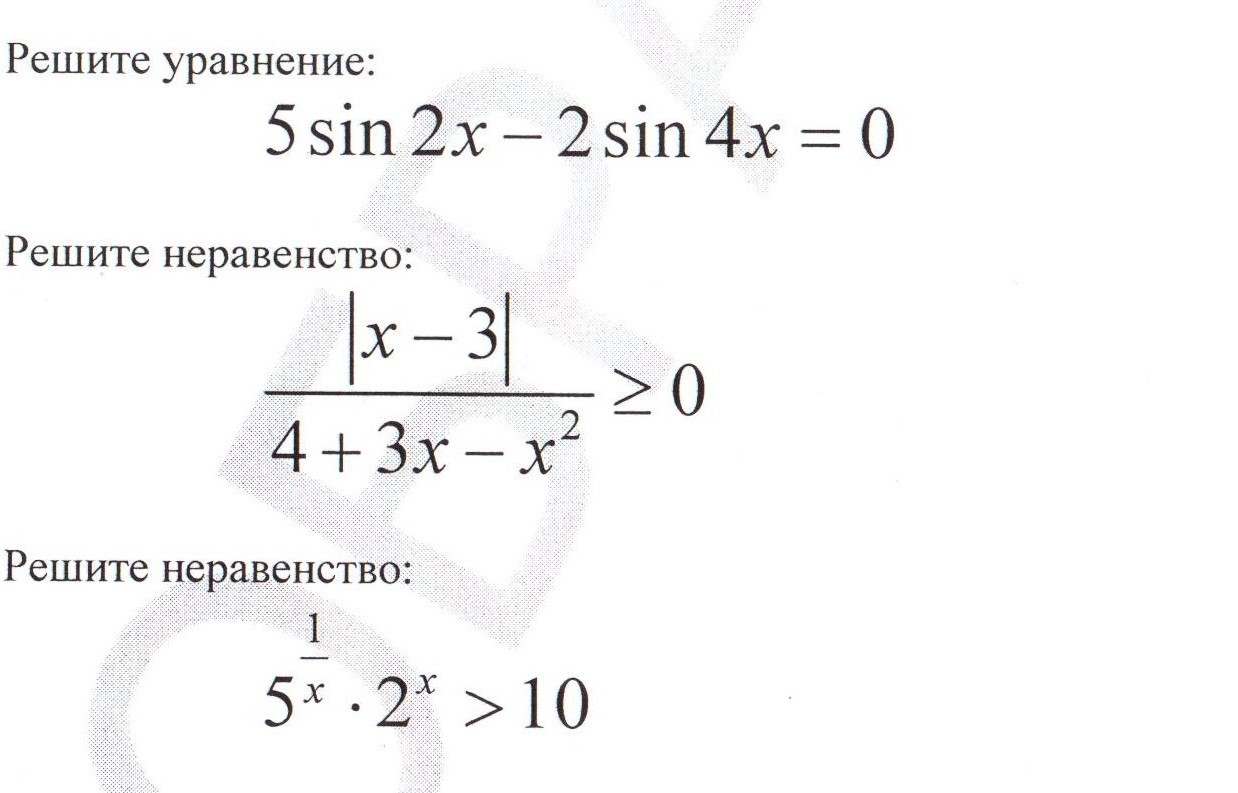Ответы
Ответ дал:
0
1) 5sin2x - sin4x = 0
5sin2x - 2sin2x*cos2x = 0
sin2x(5-2cos2x)=0 sin2x = 0 -> x = πn/2 cos2x = 5/2 (Нет решений)
Ответ: x = πn/2 n ∈ Z
2) Так как числитель всегда положителен (модуль), то наше решение равносильно решению 4+3x-x^2 ≥0 и ОДЗ x ≠ 1;4 причем x = 3 наш ответ.
Находим нули. Нули знаменателя x = 4 ; -1.
Расставляем на числовой прямой и находим знаки интервалов.
___-____-1_______+______4____-_____
Ответ: (-1 ; 4)
3)5^(1/x) * 2^x > 10
5^(1/x) * 2^x > 5 * 2 (Разделим все на 5 и на 2)
5^(1/x - 1) * 2^(x-1) > 1. Заметим, что при x > 1 наше неравенство выполняется всегда. А при x ≤ 1 не соблюдается ни при каком x , т.к. наше выражение принимает вид 1/a , где а > 1)
Ответ: x > 1
Ответ дал:
0
1) Берем производную функции. 2) приравниваем производную к нулю. 3) проставляем нули производной на числовой прямой и находим знаки интервалов. 4) там где производная положительна функция возрастает, там где отрицательна, функция убывает. Таким образом мы можем найти, например, максимальное и минимальное значение функции на заданном отрезке.
Ответ дал:
0
https://znanija.com/task/29343251 Вот пример.
Ответ дал:
0
Этот алгоритм решений и есть исследование функции с помощью производной?
Ответ дал:
0
Это лишь пример того, зачем нужна производная. Почитайте учебник анализа какой-нибудь, там все подробно должны рассказать.
Ответ дал:
0
Спасибо огромное!!
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад