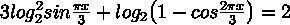Народ,помогите пожалуйста.Очень срочно надо.

3log₂²(sin(пx/3))+log₂(1-cos(2пx/3))=2

ОДЗ:

{sin(пx/3)>0 <=> 6k<x<6k+3

{1-cos(2пx/3)>0 <=> x≠3k, тогда

общее ОДЗ: 6k<x<6k+3

Так как 1-cos(2x)=2sin²x, то перепишем уравнение:

3log₂²(sin(пx/3))+log₂(2sin²(пx/3))=2

Замена: t=sin(пx/3)

3log₂²t+log₂(2t²)=2

3log₂²t+log₂2+log₂(t²)=2

3log₂²t+2log₂t-1=0

Замена: z=log₂t

3z²+2z-1=0

(z+1)(3z-1)=0

z=-1 и z=1/3

log₂t=-1 => t=1/2

log₂t=1/3 => t=∛2

sin(пx/3)=1/2

x=1/2+6k, k∈Z

x=5/2+6k, k∈Z

sin(пx/3)=∛2>1, решений нет

Ответ:

x=1/2+6k, x=5/2+6k, k∈Z