в трапеции ABCD с основаниями AD и BC угол BAD равен 30 градусам AB=6 см, BC=10см, CD=5см. Найдите длину стороны AD

ДАНО: АВСD - трапеция ; угол ВAD = 30° ; AB= 6 cм ; ВС = 10 см ; СD = 5 см

НАЙТИ: АD
_________________________

РЕШЕНИЕ:

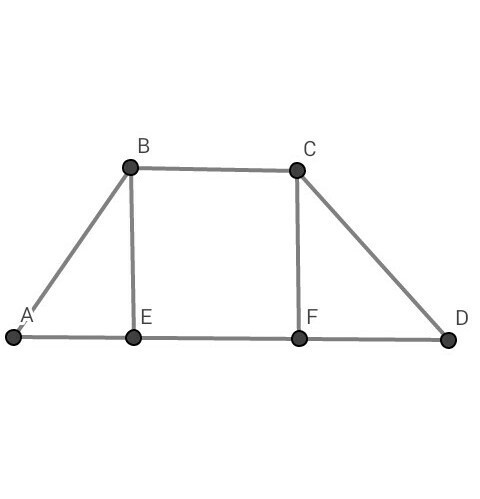
Опустим на отрезок АD две высоты ВЕ и CF:

1) Рассмотрим ∆ ВАЕ ( угол ВЕА = 90° ):

Катет, лежащий против угла в 30°, равен половине гипотенузы =>

ВЕ = 1/2 × АВ = 1/2 × 6 = 3 см

ВЕ = СF = 3 см

По теореме Пифагора:
АЕ² = АВ² - ВЕ² = 6² - 3² = 36 - 9 = 27
АЕ = 3√3 см

2 ) Рассмотрим ∆ СDF ( угол CFD = 90° ) :
По теореме Пифагора:

FD² = CD² - CF² = 5² - 3² = 25 - 9 = 16
FD = 4

AB = EF = 10 см

АD = AE + EF + FD = 3√3 + 10 + 4 = 14 + 3√3 см



ОТВЕТ: 14 + 3√3 см

Упс. AB(6)=EF=10, ой, не корректно.

Это не " не корректно " . Это незначительная ошибка. У меня таких полно :)

Вижу Вы мситите тем, кто недооценил вашу работу )

Может быть, проверите остальные задания. А то у меня времени нет.