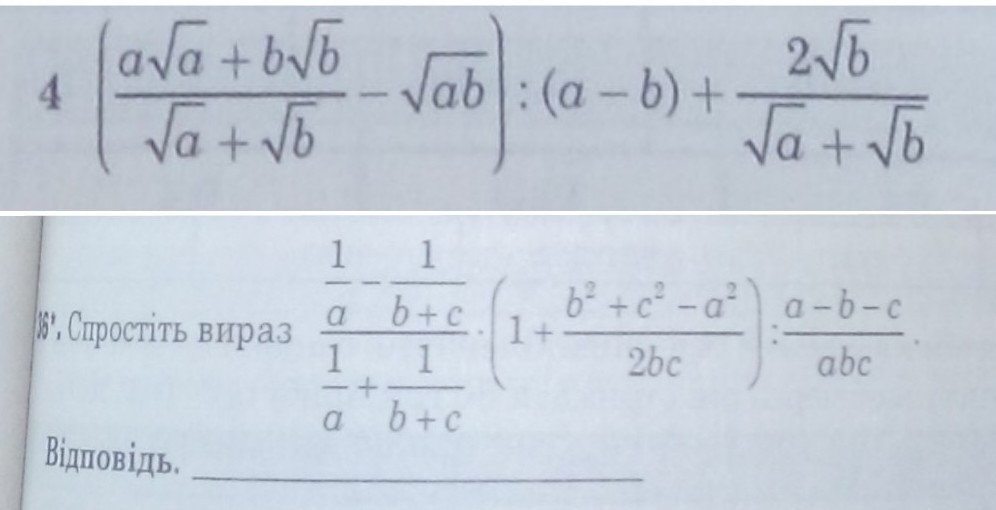• Предмет: Алгебра
  • Автор: darina9081
  • Вопрос задан 7 лет назад
< >

Помогите пожалуйста!!! Очень срочно!!! Решить по действиях, примеры 4 и 36

Приложения:

Ответы

Ответ дал: NNNLLL54
0

4); ; (frac{asqrt{a}+bsqrt{b}}{sqrt{a}+sqrt{b}}-sqrt{ab}):(a-b)+frac{2sqrt{b}}{sqrt{a}+sqrt{b}}=\\=(frac{(sqrt{a}+sqrt{b})(a-sqrt{ab}+b)}{sqrt{a}+sqrt{b}}-sqrt{ab})cdot frac{1}{(a-b}+frac{2sqrt{b}}{sqrt{a}+sqrt{b}}=\\=frac{a-2sqrt{ab}+b)}{(sqrt{a}-sqrt{b})(sqrt{a}+sqrt{b})}+frac{2sqrt{b}}{sqrt{a}+sqrt{b}}=frac{(sqrt{a}-sqrt{b})^2}{(sqrt{a}-sqrt{b})(sqrt{a}+sqrt{b})}+frac{2sqrt{b}}{sqrt{a}+sqrt{b}}=\\=frac{sqrt{a}-sqrt{b}}{sqrt{a}+sqrt{b}}+frac{2sqrt{b}}{sqrt{a}+sqrt{b}}=frac{sqrt{a}-sqrt{b}+2sqrt{b}}{sqrt{a}+sqrt{b}}=frac{sqrt{a}+sqrt{b}}{sqrt{a}+sqrt{b}}=1

36); ; frac{frac{1}{a}-frac{1}{b+c}}{frac{1}{a}+frac{1}{b+c}}cdot (1+frac{b^2+c^2-a^2}{2bc}}):frac{a-b-c}{abc}=\\=frac{b+c-a}{b+c+a}cdot frac{(2bc+b^2+c^2)-a^2}{2bc}cdot frac{abc}{a-b-c}=\\=frac{-(a-b-c)}{a+b+c}cdot frac{(b+c)^2-a^2}{2bc}cdot frac{abc}{a-b-c}=frac{-1}{a+b+c}cdot frac{(b+c-a)(b+c+a)}{2bc}cdot frac{abc}{1}=\\=frac{-1cdot (b+c-a)cdot a}{2}=frac{acdot (a-b-c)}{2}

Ответ дал: miron2077
0

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Приложения:
Ответ дал: NNNLLL54
0
В 5 пункте №36 не дописали (a+b+c) в знаменатель
Ответ дал: miron2077
0
Спасибо! Увидел, исправил, правда, грязновато получилось
Похожие вопросы
Русский язык
2 года назад
Подчеркни глаголы в неопределенной форме. Как отличишь их? Какие два из них отвечают не на тот вопрос, что другие? Свойство зеркальце имело: Говорить оно умело… “Ты, царица, всех милее, Всех
Русский язык
2 года назад
выпиши две группы слов:1)слова,в которых безударные гласные можно проверить;2)слова с непроверяемой гласной. Для своей работы художник осень взяла самые яркие краски и прежде всего отправилась с ними
Математика
2 года назад
ПОМОГИТЕ ПОЖАЛУЙСта! 4. В магазин привезли белые, синие и зеленые рубашки. Белых рубашек 39 шт и их количество составляет 61 часть от количества синих рубашек. Какой процент от всех привезенных в
Информатика
2 года назад
1) Напишите программу, которая получает четырёхзначное число и определяет, верно ли, что оно является палиндромом (программа должна вывести ответ «да» или «нет»). Например, число 2332 – палиндром, а
Математика
8 лет назад
У Оксаны было 72 конфеты.Все конфеты она раздал детям, каждый ребенок получил 3 шоколадных конфеты и 5 карамель. Сколько шоколадных конфет было у Оксаны сначала?
Математика
8 лет назад
найди правило по которому из двух чисел записанных внизу получено число записанное вверху. Запиши нужное число в окошко в третьем круге
Информатика
9 лет назад
Учитывая, что текст представлен в расширенном ASCII коде, определите приблизительное количество информации в диктанте, который был написан за 10 минут учеником, способным написать около 200 знаков в
Биология
9 лет назад
Помогите таблица ПАРАЗИТИЧЕСКИЕ ПРОСТЕЙШИЕ : 1 название паразита; 2 поражаемые органы животного или человека; 3 причиняемый вред.