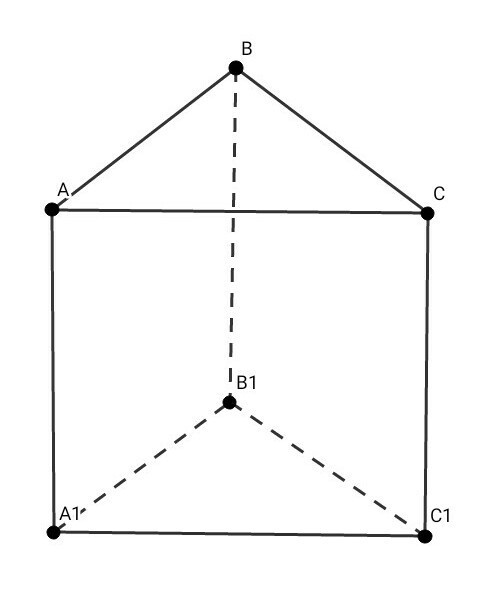
Треугольник ABC со сторонами 10, 17 и 21, является основанием прямой призмы ABCA1B1C1 . Площадь основания призмы равна площади наименьшей боковой грани. Найдите объем призмы.

ДАНО: АВСА1В1С1 - прямая треугольная призма ; АВ = 10 ; ВС = 17 ; АС = 21 ; S abc = S ( наим. бок. грани )

НАЙТИ: V ( призмы )
_______________________

РЕШЕНИЕ:

1) Рассмотрим ∆ АВС :

Найдём площадь ∆ АВС по формуле Герона :


Где а, b, c - стороны треугольника ; р = ( a + b + c ) / 2 - полупериметр



2) Так как все боковые грани данной призмы имеют одинаковую высоту, равную боковому ребру, то наименьшую площадь имеет та боковая грань, у которой наименьшее основание, то есть та, которая содержит наименьшую сторону ∆ АВС

Значит, грань АВВ1А1 - это наименьшая по площади грань призмы.

S abb1a1 = S abc = 84

3) Все боковые грани прямой призмы являются прямоугольниками =>

S abb1a1 = А1В1 × АА1

84 = 10 × АА1

АА1 = 84 : 10 = 8,4

4) V ( призмы ) = S abc × AA1

V ( призмы ) = 84 × 8,4 = 705,6

ОТВЕТ: V ( призмы ) = 705,6