Задание №229:
Найдите произведение целых значений х из области определения функции
$y = sqrt{-3x-9} +frac{1}{sqrt{2x+12}}$ .

Задание №234:
Дан график функции (внизу в файле) $f(x)=ax^{2}+bx+c$ . Какое из соотношений верно?
А) $frac{b}{2a} textless 0$
Б) $b^{2} -4ac=0$
В) $a+b+c=0$
Г) $frac{c}{a} textless 0$
Д) $frac{ac}{b} textgreater 0$

П.С.: Друзья, прошу вас дать полный ответ с решениями.

Приложения:

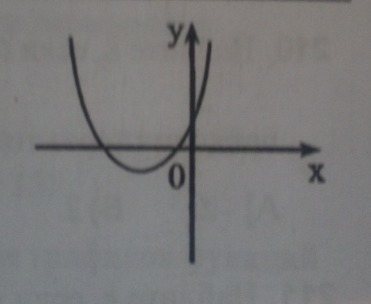
Ответы

Ответ дал: Artem112

229.

$y = sqrt{-3x-9} +frac{1}{sqrt{2x+12}}$

ООФ:

$left{begin{array}{l} -3x-9geq 0 \ 2x+12>0 end{array} Rightarrow<br />left{begin{array}{l} -3xgeq 9 \ 2x>-12 end{array} Rightarrow<br />left{begin{array}{l} xleq-3 \ x>-6 end{array}$

$Rightarrow xin(-6;-3]$

Произведение целых значений:

$(-5)cdot(-4)cdot(-3)=-60$

Ответ: -60

234.

Проверяем соотношения по очереди:

$frac{b}{2a} <0$ - можно заметить, что выражение в левой части противоположно абсциссе вершины параболы. Вершина лежит в левой полуплоскости, значит данное выражение положительно. Не подходит. (Либо можно сказать про знаки коэффициентов a>0, b>0, откуда сделать такой же вывод).

$b^2-4ac=0$ - в левой части стоит выражение для дискриминанта. Нулевой дискриминант показывает одну точку пересечения параболы с осью х, когда на рисунке их две. Не подходит.

$a+b+c=0$ - при нулевой сумме коэффициентов один из корней равен 1, однако на рисунке оба корня отрицательных. Не подходит. (Либо сказать a>0, b>0, с>0, значит сумма таких чисел положительна).

$frac{c}{a} textless 0$ - а>0, так как ветви параболы направлены вверх, с>0, так как такое значение имеет функция при х=0, значит и отношение двух положительных чисел положительно. Не подходит.

$frac{ac}{b} textgreater 0$ - а и с положительны, b>0 по теореме Виета, так как парабола ветвями вверх имеет два отрицательных корня. Значит, такое соотношение соотношение для трех положительных чисел положительно.