Геометрическая прогрессия

Приложения:

Ответы

Ответ дал: mishka19

$1) c_1=5\ c_2=5^2$

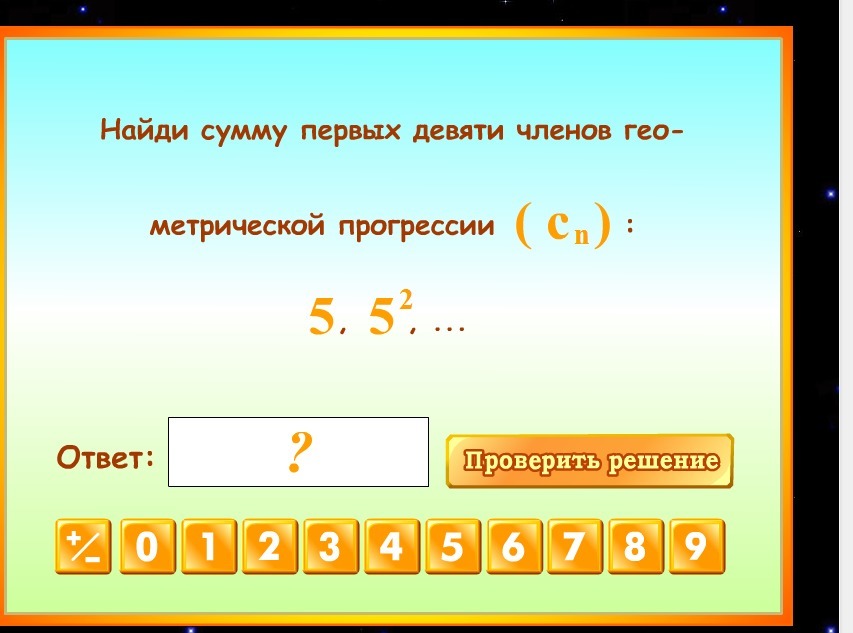
Знаменатель геометрической прогрессии равен отношению последующего члена этой прогрессии к предыдущему:

$q=frac{c_2}{c_1}=frac{5^2}{5} =5$

Формула суммы n первых членов геометрической прогрессии:

$S_n=frac{c_1cdot(q^n-1)}{q-1}$

Тогда

$S_9=frac{5cdot(5^{9}-1)}{5-1}=frac{5cdot(1953125-1)}{4}= frac{5cdot(1953124}{4}=5cdot488281=2441405$

Ответ: 2441405

$2)c_5=128\ q=2$

Формула n-го члена геометрической прогрессии: $c_n=c_1cdot q^{n-1}$

Тогда $c_5=c_1cdot q^{5-1}=c_1cdot q^4$

Откуда $c_1=frac{c_5}{q^4}=frac{128}{2^4}=frac{2^7}{2^4}=2^3=8$

Формула суммы n первых членов геометрической прогрессии:

$S_n=frac{c_1cdot(q^n-1)}{q-1}$

Тогда

$S_7=frac{8cdot(2^7-1)}{2-1}=frac{8cdot(128-1)}{1}=8cdot127=1016$

Ответ: 1016

Похожие вопросы

Русский язык

2 года назад

Английский язык

2 года назад

Литература

2 года назад

Математика

2 года назад

Математика

8 лет назад

Физика

8 лет назад

Математика

9 лет назад

Алгебра

9 лет назад