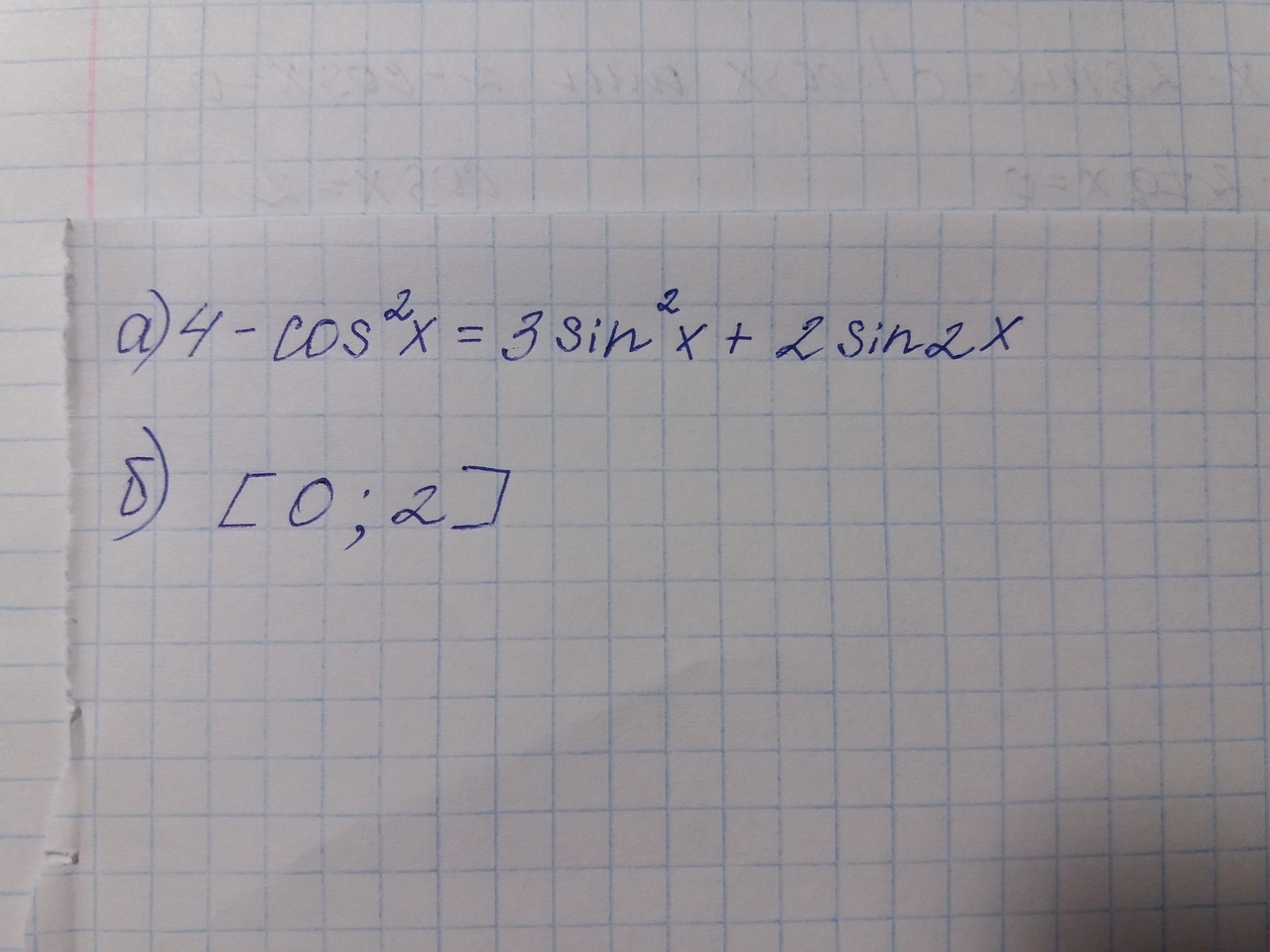Предмет: Алгебра
Автор: viktoriya365
Вопрос задан 7 лет назад

Помогите с тригонометрией ,пожалуйстааа

Приложения:

Ответы

Ответ дал: snow99

$4 - {cos}^{2} x = 3 {sin}^{2} x + 2sin2x \ 4 {sin}^{2} x + 4{cos}^{2} x - {cos}^{2} x = 3 {sin}^{2} x + 4sinxcosx \ {sin}^{2} x - 4sinxcosx + 3 {cos}^{2} x = 0 \$
Разделим всё уравнение на cos^2x, получаем:
${tg}^{2} x - 4tgx + 3 = 0 \ tgx = t \ {t}^{2} - 4t + 3 = 0 \ 1)t1 = 1 \ tgx = 1 \ x = frac{pi}{4} + pi n \ 2)t2 = 3 \ tgx = 3 \ x = arctg3 + pi n$

б) Найдем корни на указанном отрезке: [0; 2].
$x = frac {pi}{4} \<br />x = arctg3$

Ответ дал: snow99

основное тригонометрическое тождество sin^2x + cos^2x = 1, а у нас 4, тогда мы можем записать 4sin^2x + 4cos^2x

Ответ дал: Аноним

на отрезке нужно корни отобрать

Ответ дал: snow99

А может, там нужно найти количество или наибольший/наименьший положительный/отрицательный. Условие не сформулировано.

Ответ дал: viktoriya365

Нет,корни на отрезке

Ответ дал: snow99

Дописано

Ответ дал: NNNLLL54

$4-cos^2x=3sin^2x+2sin2x\\4underbrace {(sin^2x+cos^2x)}_{1}-cos^2x=3sin^2x+2cdot 2, sinxcdot cosx\\4sin^2x+3cos^2x-3sin^2x-4sinxcdot cosx=0\\sin^2x-4sinxcdot cosx+3cos^2x=0; |:cos^2xne 0\\tg^2x-4, tgx+3=0\\t=tgx; ,; ; t^2-4t+3=0; ,; ; t_1=1; ,; t_2=3; ; (teorema; Vieta)\\a); ; tgx=1; ,; ; x=frac{pi }{4}+pi n,; nin Z\\b); ; tgx=3; ,; x=arctg3+pi k,; kin Z\\c); ; xin [, 0,2, ]:; ; x=frac{pi }{4}; ,; ; x=arctg3; ; ; (2; radapprox 115^circ )$