Предмет: Математика
Автор: rignuvilte
Вопрос задан 7 лет назад

< >

АО = 5
АВ = 12
Найти х

Приложения:

Ответы

Ответ дал: inga21yaltap8df66

0

Решение на фотографии

Приложения:

Ответ дал: ilmarr

0

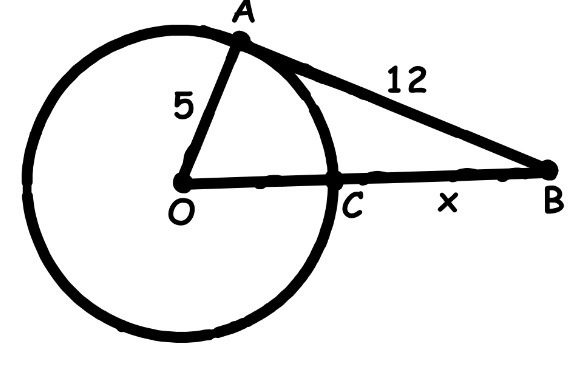
Так как АБ лежит на касательной к окружности, то радиус ОА к нему перпендикулярен, 90 градусов. Из этого следует что

$|OB|^{2} = |OA|^{2} + |AB|^{2} \ |OB| = sqrt{|OA|^{2} + |AB|^{2}} \ |OB| = sqrt{5^{2} + 12^{2}} = sqrt{25 + 144} = sqrt{169} = 13 \ \<br /><br />$ Теперь от |ОБ| надо отнять |ОС|, учитывая что |ОС|=|ОА|=5, т.к. это радиус окружности:

$x= |OB|-|OC|= 13 - 5 = 8 \$

Приложения:

Похожие вопросы

Русский язык

2 года назад

нужно текс в разговорном ,научном, художествином стили речи

Русский язык

2 года назад

Найдите суффикс в слове Ученик

Литература

2 года назад

Для тех, кто внимательно читал 1. Каким ты представляешь себе мельника Панкрата? 2. Почему ребята считали его колдуном? 3. Какой характер у Панкрата?

Математика

2 года назад

-12x>48 помогите пожалуйста решить

География

8 лет назад

Современные процессы формирования рельефа

История

8 лет назад

Определите суть нарицательного в русском языке истории понятия семибоярщина

Обществознание

9 лет назад

какие изменения происходят с человеком в подростковом возрасте. При затруднение с ответом обратись к тексту учебника ,где говориться о таких изменениях .

Математика

9 лет назад

Вынесите общий множитель за скобки : а)8*3+8*2, б)8*3+5*3, в)9*13+7*9, г) 27*3+3*2 Ребята! это срочно! эти * значит умножение