В трапеции ABCD с основаниями
BC=20 и AD=70 проведена прямая , параллельная основаниям трапеции и пересекающая боковые ребра AB и CD соответственно в точках E и F. Найдите EF, если CF:FD=2:3.
Ответы
Ответ дал:
0
Рассмотрим треугольники TCF и ACD, угол C для них общий, углы CAD и CTF равны друг другу как соответственные углы при параллельных прямых, следовательно треугольники TCF и ACD подобны.
То есть: TF/AD = CF/CD = CF/CF+DF = 2/5
Из этого: TF = 2/5 x 70 = 28.
Аналогичным образом из треугольников ETA и ABC можем узнать, что:
ET = BC x 2/5 = 2/5 x 20 = 8.
Таким образом, EF = ET + TF = 8+28 = 36.
Ответ: EF = 36.
Приложения:
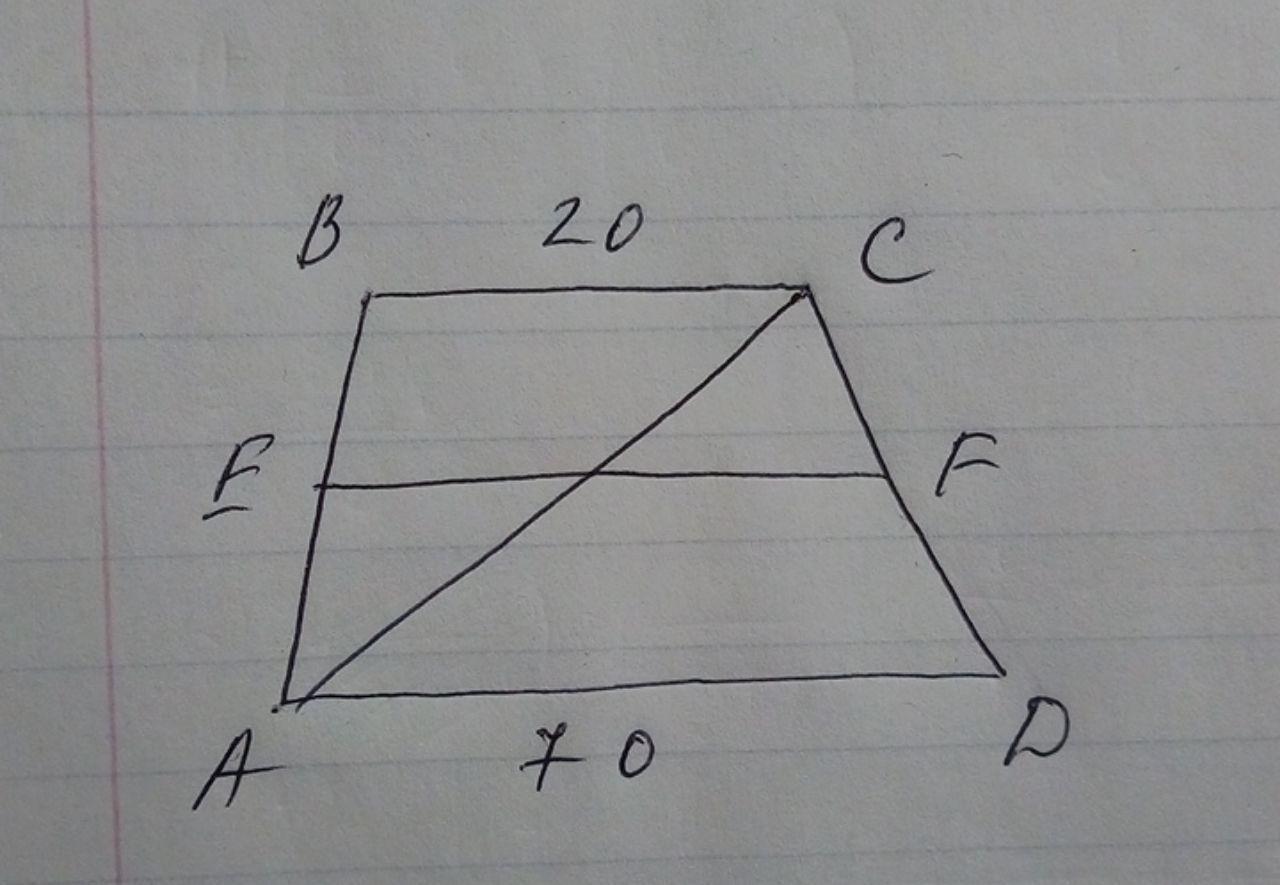
Ответ дал:
0
Где точка Т ?
Ответ дал:
0
Точка Т это точка пересечения AC и EF.
Ответ дал:
0
Трапеция с равными углами при основаниях
Верхнее =20
Нижнее =70
Разница =50
Соотношение в сумме равно 5
Разницу делим на соотношение и получаем пять частей по 10 см - это расстояние между теоретическими линиями между основаниями, нам нужна та, что находится в 20 см от верхнего основания =>
EF = 40 см
Верхнее =20
Нижнее =70
Разница =50
Соотношение в сумме равно 5
Разницу делим на соотношение и получаем пять частей по 10 см - это расстояние между теоретическими линиями между основаниями, нам нужна та, что находится в 20 см от верхнего основания =>
EF = 40 см
Приложения:
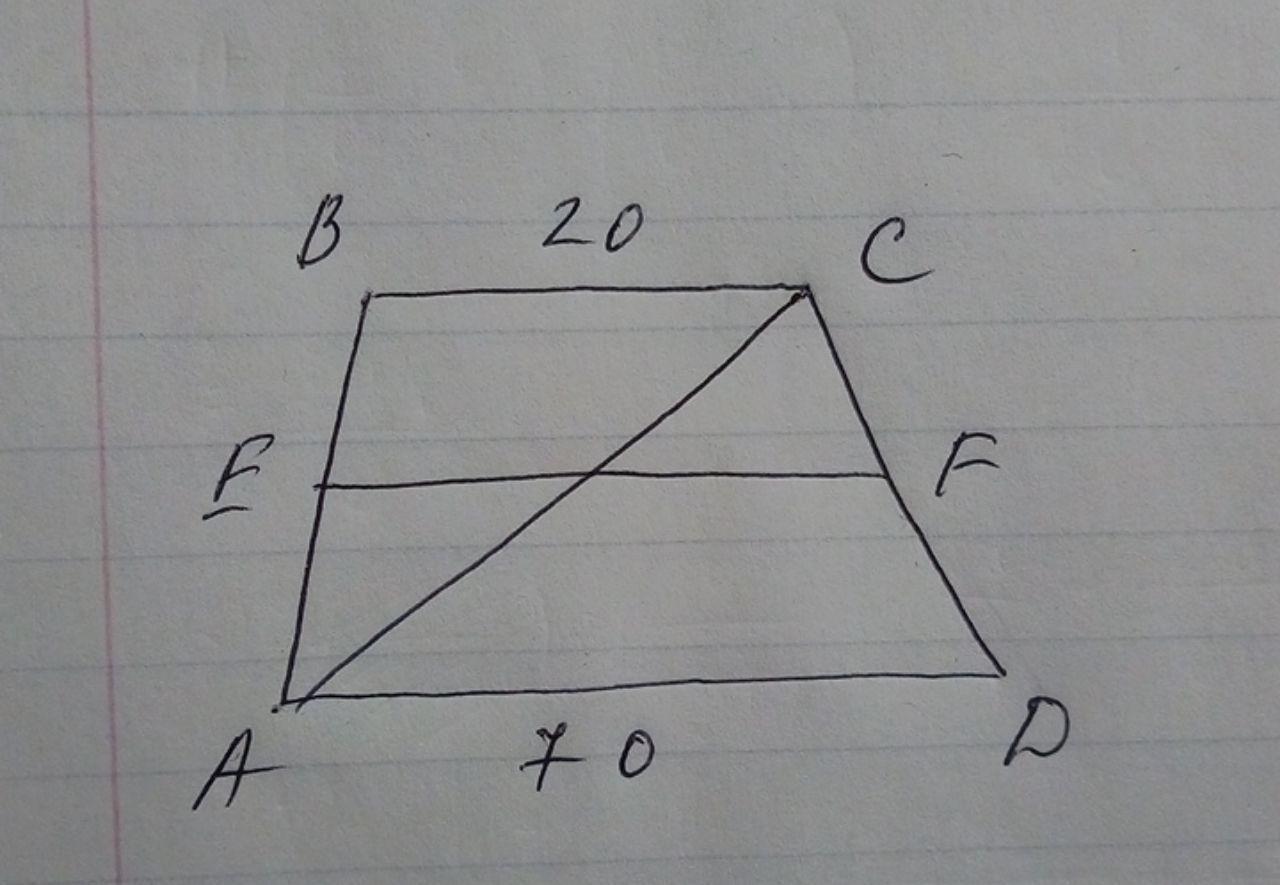
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад