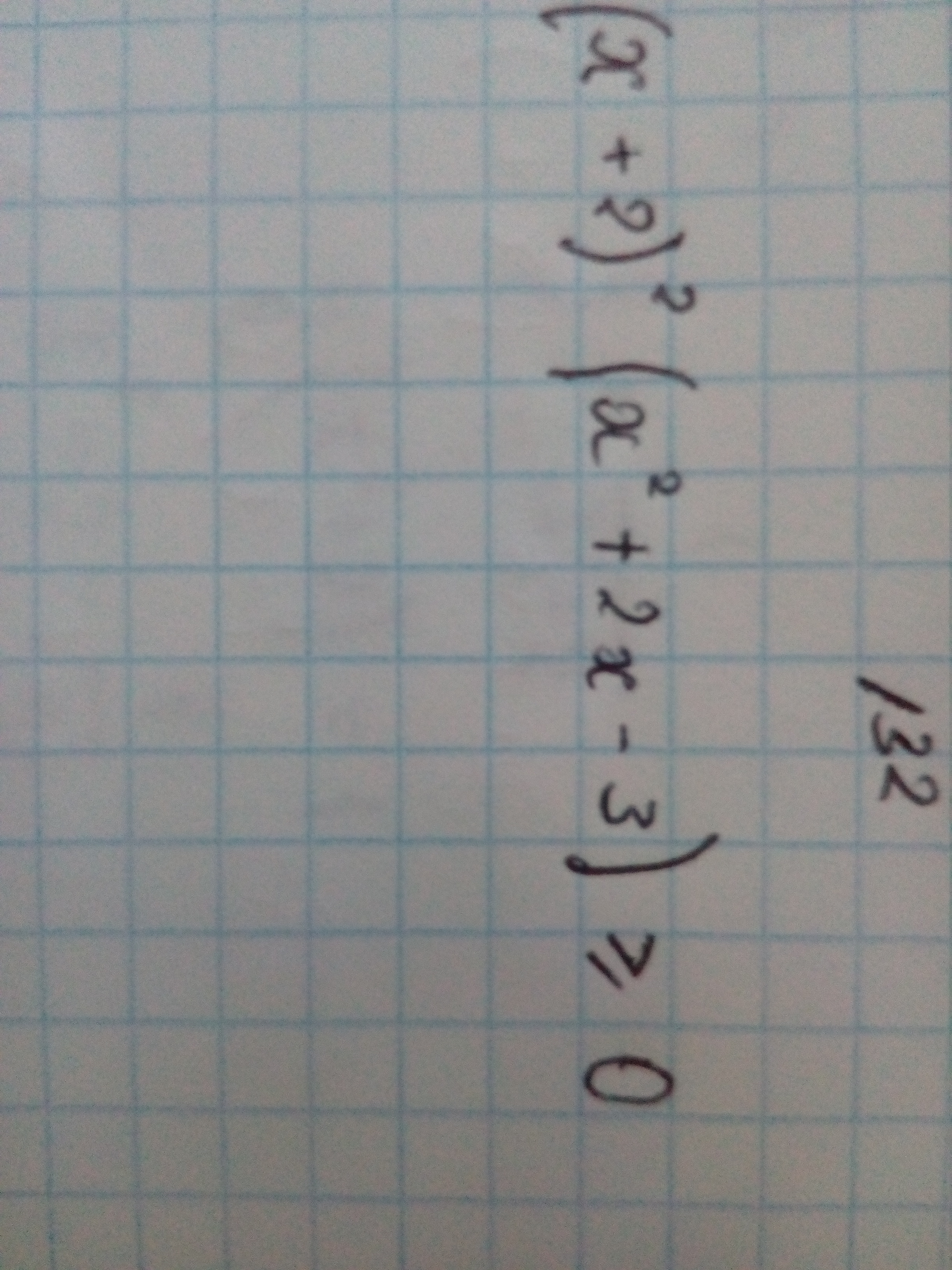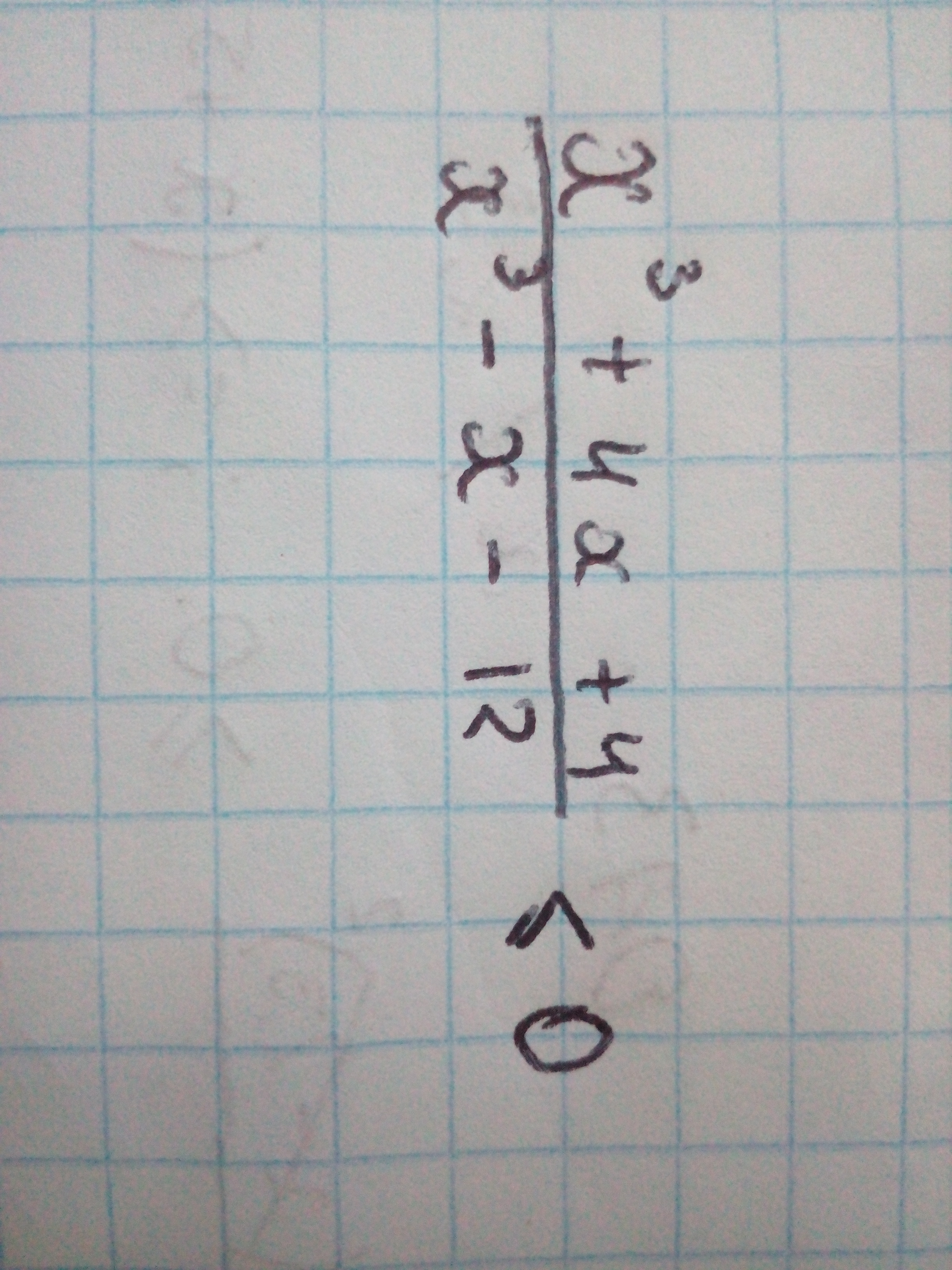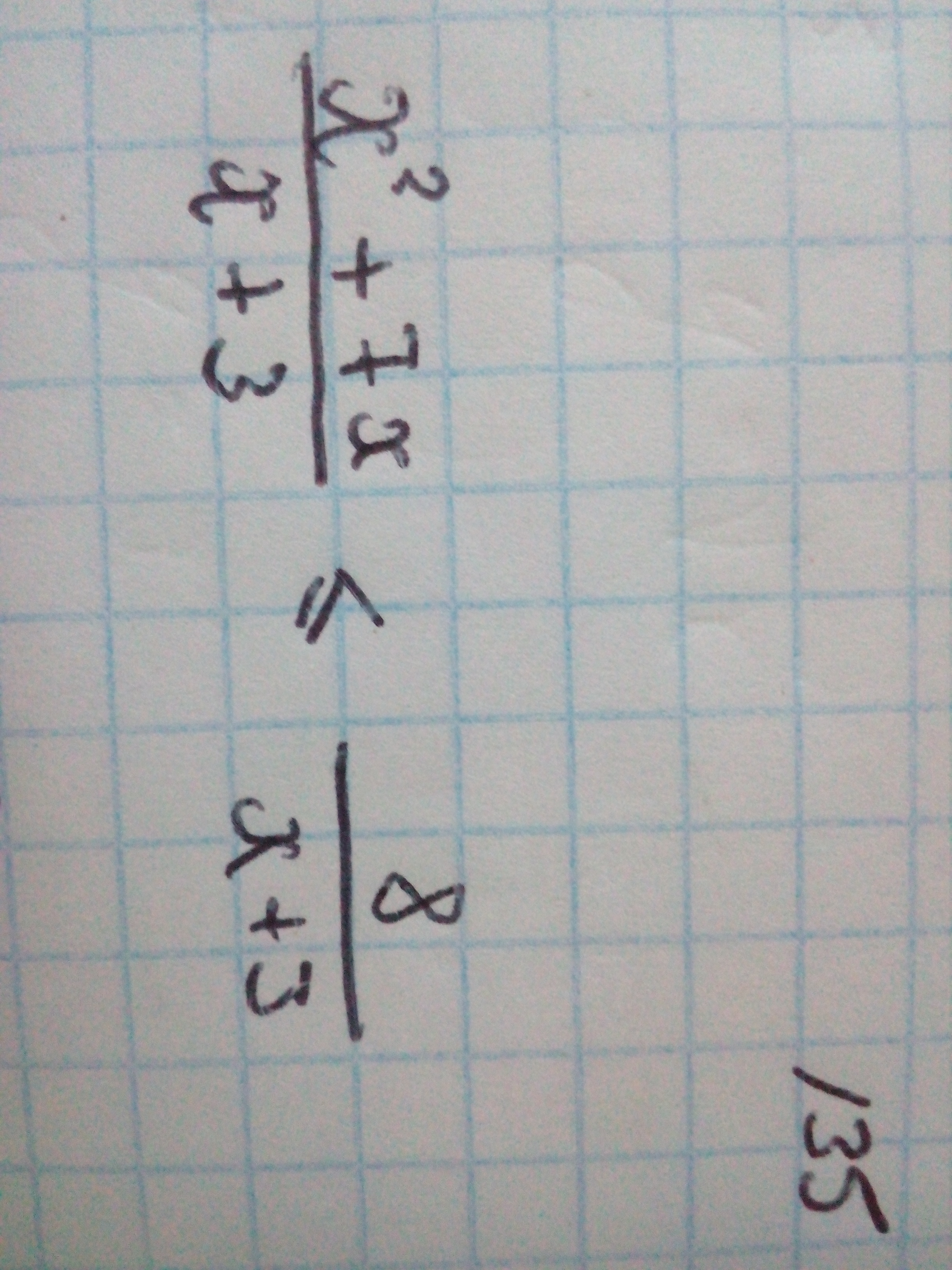Решить методом интервалов

метод интервалов предполагает разложение на множители...

№132) корни (-2) и по т.Виета (-3) и (1); корень (-2) кратный(четный показатель степени), при переходе через него функция знак не изменит...

+++++++[-3]--------[-2]--------[1]++++++(ось ОХ) x∈(-oo; -3] U {-2} U [1; +oo)

№135) если перенести все в левую часть неравенства и сложить дроби (у них уже знаменатель общий); получим дробь: в числителе х²+7х-8 (корни по т.Виета (-8) и (1)); знаменатель не изменится х+3 (корень (-3));

--------[-8]+++++++(-3)--------[1]++++++(ось ОХ) x∈(-oo; -8] U (-3; 1]

а в третьем примере точно нет опечатки? там третья степень для х ?