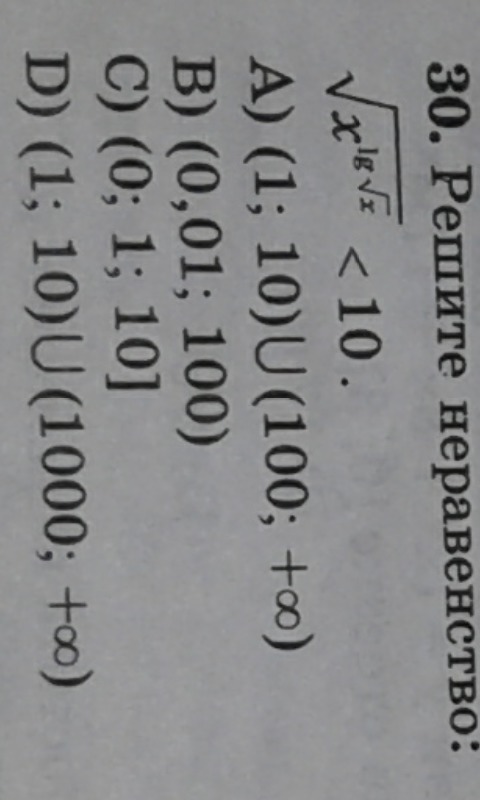Предмет: Математика
Автор: bestmusic
Вопрос задан 8 лет назад

< >

Помогите решить неравенство пожалуйста

Приложения:

Ответы

Ответ дал: alkorb

0

ОДЗ: x>0

для начала заменим знак неравенства на равно, возведем обе части в квадрат и найдем корни полученного уравнения методом логарифмирования:

$sqrt{x^{lgsqrt{x}}} =10 \ \ x^{lgsqrt{x}}=100 \ \ lg(x^{lgsqrt{x}})=lg100\ \lgsqrt{x} *lgx=2 \ \ lgx^{frac{1}{2} }*lgx=2 \\ frac{1}{2}*lgx*lgx=2 \ \lg^2x=4 \ \ lgx=^+_-2 \ \ begin{bmatrix}x=10^{-2}\x=10^2end{matrix} Leftrightarrow begin{bmatrix}x=0.01\x=100end{matrix}$

Теперь, для решения неравенства, воспользуемся методом интервалов:

$sqrt{x^{lgsqrt{x}}} <10 \ sqrt{x^{lgsqrt{x}}} -10 <0 \ \ +++(0.01)---(100)+++>_x \ \ x in (0.01; 100) \ \ OTBET: B)$

Похожие вопросы

Окружающий мир

2 года назад

Что относится к не рудным полезным ископаемым а)соль,гранит,песок,глина б) медная руда,железная руда в) каменный уголь,нефть,газ

Қазақ тiлi

2 года назад

Суретте 2-3балалар коньки теуып жур.Соган ангиме курау

Математика

2 года назад

Помогите решить на рисунке номера. МЕНЯ МАМА УБЬЕТ

Физика

2 года назад

Помогите срочно нужно!!!

История

8 лет назад

помогите пожалуйста!! Сообщение в тетради на тему: значение эпохи нового времени! пожалуйста очень надо завтра в школу

Физика

8 лет назад

Почему мокрая газета рвётся значительно легче, чем сухая?

Математика

9 лет назад

решите числовой ребус ААА+AA+A=BB зарание спасибо

Математика

9 лет назад

что называется медиатрисой отрезка?