Дан куб АВСДА1В1С1Д1. На его ребрах АА1 В1С1 выбрали точки N и K соответственно так, что AN=B1K.
а) Докажите, чтот прямые NK и D1B перпендикулярны.
б) Наидите двугранный угол при ребре NK тетраэдра NKBD1, если AN:NA1=1:4

..........................................

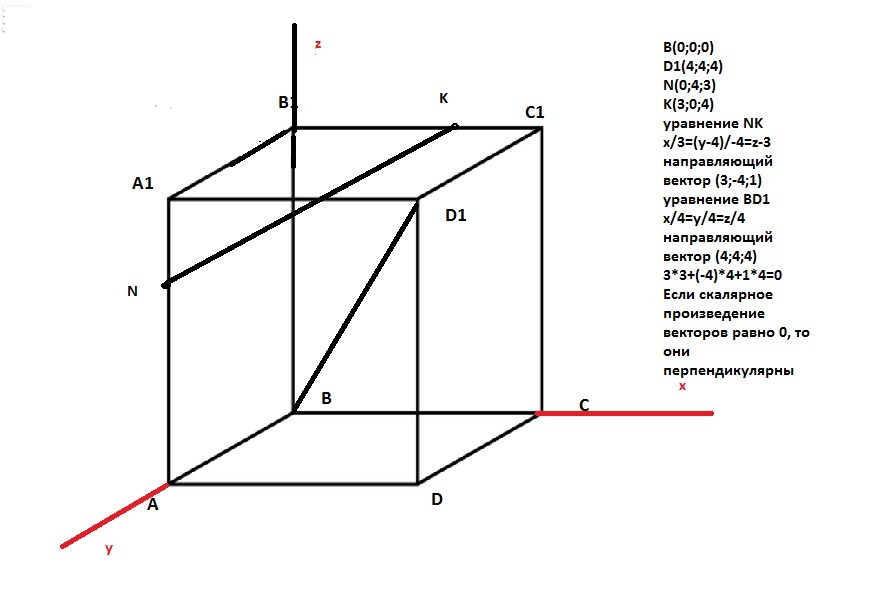
Пусть куб единичный.

Пусть A- начало координат

Ось X - AB

Ось Y - AD

Ось Z - AA1

1) Пусть AN=B1K=a

Координаты точек

N(0;0;a)

K(1;a;1)

D1(0;1;1)

B(1;0;0)

Вектора

NK(1;a;1-a)

D1B(1;-1;-1)

NK*D1B = 1 -a -1 + a = 0 Значит перпендикулярны . Доказано.

2)

N(0;0;0.2)

K(1;0.2;1)

D1(0;1;1)

B(1;0;0)

Уравнение плоскости NKB

ax+by+cz+d=0

подставляем координаты точек

0.2с+d=0

a+0.2b+с+d=0

a+d=0

Пусть d = -1 тогда с= 5 a =1 b= -25

Уравнение

x-25y+5z-1=0

Уравнение плоскости NKD1

ax+by+cz+d=0

подставляем координаты точек

0.2с+d=0

a+0.2b+с+d=0

b+c+d=0

Пусть d= -1 тогда с = 5 b= -4 a= -3.2

Уравнение

-3.2x-4y+5z-1=0

Косинус угла между плоскостями

(-3.2+100+25) / √(1+625+25) / √( 10.24+16+25) = 609 / √(833931) = 29 / √1891

Искомый угол тупой как видно из рисунка

Угол равен arccos( -29 / √1891)