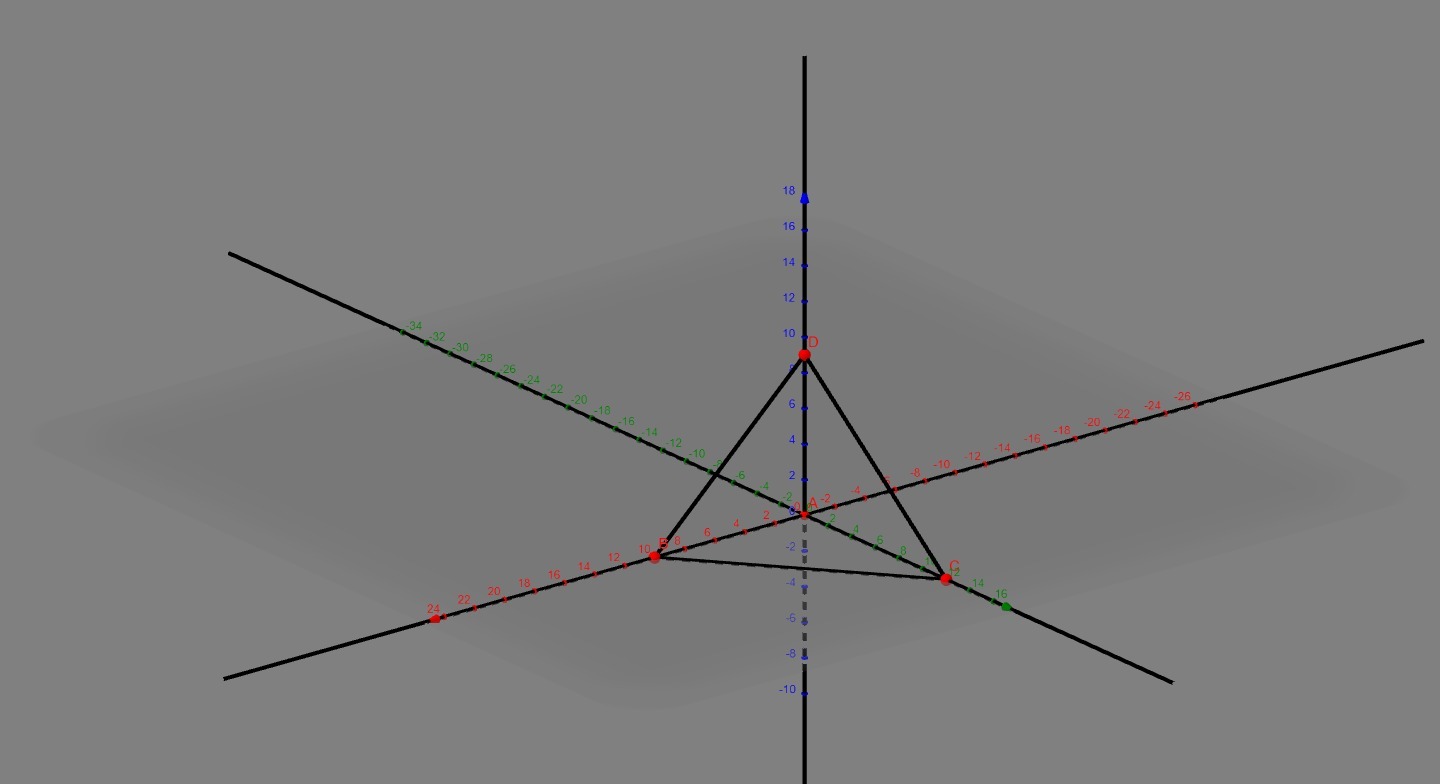
даны 3 взаимно перпендикулярные прямые ав,ас и ад. найти меньший угол треугольника всд, если ад=9см,дс=10 см;вд=12 см
Ответы
Ответ дал:
0
Т.к. прямые взаимно перпендикулярны, то треугольники BAD, CAD и CAB прямоугольные. По теореме Пифагора найдём AB=(100-81)^(1/2)=19^(1/2), а AC=(144-81)^(1/2)=63^(1/2), после найдём BC=(19+63)^(1/2)=82^(1/2). В итоге у мы определили стороны треугольника BCD: BC=82^(1/2), BD=12, CD=10 (см), в итоге нам надо найти угол BDC, т.к. против меньшей стороны лежит меньший угол. Его найдём по теореме косинусов: cos(BDC) = 27/40, а угол BDC = acrcos27/40
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
9 лет назад